Maximum principles and bounds for initial value problems
The previous post looked at using maximum principles to bound the solution to a boundary value problem. This is a similar post, focusing on an initial value problem. As before we start with the differential operator
L[u] = u" + g(x)u' + h(x)
where g and h are bounded and h is non-positive. We are interested in solutions to the equation L[u] = f, but this time we want to specify the initial conditions u(0) = u'0 and u(0) = u'0. We will use the same maximum principle as before, but a slightly different approach to constructing upper and lower bounds on solutions. Our conclusion will also be a little different: this time we'll get upper and lower bounds not only on the solution u but also on its derivative u'.
We look for a function z(x) satisfying the differential inequality
L[u] a f
and the two initial inequalities z(0) a u'0 and z(0) a u'0. We also look for a function w(x) satisfying the same inequalities in the opposite direction, i.e. replacing a with a. (Note that replacing equality with inequality in the differential equation and initial conditions makes it much easier to find solutions.)
The maximum principle tells us that z and w provide upper and lower bounds respectively on u, and their derivatives provide bounds on the derivative of u. That is,
w(x) a u(x) a z(x)
and
w'(x) a u'(x) a z'(x).
We illustrate this technique on a variation on Bessel's equation:
u"(x) + u'(x)/x - u(x) = 0
with initial conditions u(0) = 1 and u'(0) = 0. We wish to bound the solution u on the inverval [0, 1].
As candidates, we try z = c1x2 + 1 and w = c2x2 + 1. (Why not a general quadratic polynomial? The initial conditions tell us that the linear coefficient will be 0 and the constant term will be 1.)
Since
L[cx2 + 1] = c(4 - x2) - 1
it suffices to pick c1 = 1/3 and c2 = 1/4. This tells us that
x/4 + 1 a u(x) a x/3 + 1.
To see how well these bounds work, we compare with the exact solution I0, the so-called modified Bessel function of the first kind.
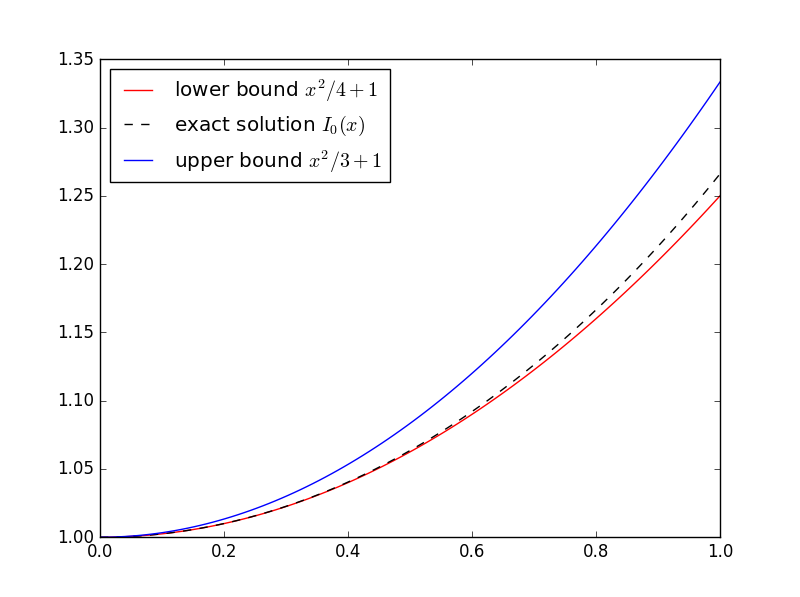
The lower bound is very good, though a comparably good upper bound would take a more careful choice of z.
Source: Maximum Principles in Differential Equations by Protter and Weinberger
Related posts:
- Relations between Bessel functions
- Maximum principles and bounds for boundary value problems
- Partial differential equations