Cornu’s spiral

Cornu's spiral is the curve parameterized by

where C and S are the Fresnel functions, sometimes called the Fresnel cosine integral and Fresnel sine integral. Here's a plot of the spiral.

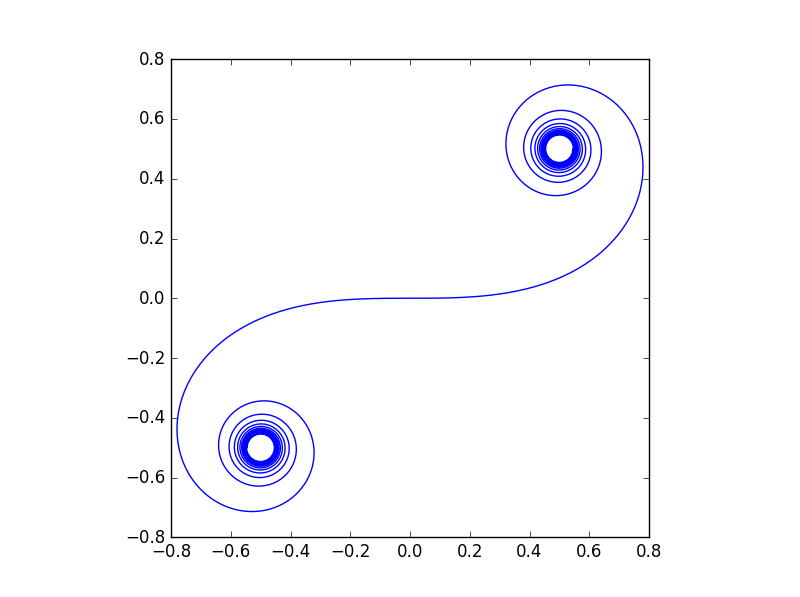
Both Fresnel functions approach as t a' a and so the curve slowly spirals toward (, ) in the first quadrant. And by symmetry, because both functions are odd, the curve spirals toward (-, -) in the third quadrant.

Here's the Python code used to make the plot.

 from scipy.special import fresnel from scipy import linspace import matplotlib.pyplot as plt t = linspace(-7, 7, 1000) y, x = fresnel(t) plt.plot(x, y) plt.axes().set_aspect("equal") plt.show()

The SciPy function fresnel returns both Fresnel functions at the same time. It returns them in the order (S, C) so the code reverses the order of these to match the Cornu curve.

One interesting feature of Cornu's spiral is that its curvature increases linearly with time. This is easy to verify: because of the fundamental theorem of calculus, the Fresnel functions reduce to sines and cosines when you take derivatives, and you can show that the curvature at time t equals It.

How fast does the curve spiral toward (, )? Since the curvature at time t is It, that says that at time t the curve is instantaneously bending like a circle of radius 1/It. So the radius of the spiral is decreasing like 1/It.

Cornu's spiral was actually discovered by Euler. Cornu was an engineer who independently discovered the curve much later. Perhaps because Cornu used the curve in applications, his name is more commonly associated with the curve. At least I've more often seen it named after Cornu. This is an example of Stigler's law that things are usually not named after the first person to discover them.