Positive polynomials and squares

If a real polynomial in one variable is a sum of squares, it obviously cannot be negative. For example, the polynomial

p(x) = (x² - 3)² + (x + 7)²

is obviously never negative for real values of x. What about the converse: If a real polynomial is never negative, is it a sum of squares? Yes, indeed it is.

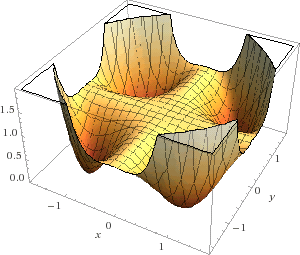
What about polynomials in two variables? There the answer is no. David Hilbert (1862-1943) knew that there must be positive polynomials that are not a sum of squares, but no one produced a specific example until Theodove Motzkin in 1967. His polynomial

p(x, y) = 1 - 3x²y² + x²y⁴ + x⁴y²

is never negative but cannot be written as a sum of any number of squares. Here's a plot:

Source: Single Digits