Tensors 1: What is a tensor?
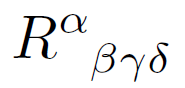
The word "tensor" is shrouded in mystery. The same term is applied to many different things that don't appear to have much in common with each other.
You might have heared that a tensor is a box of numbers. Just as a matrix is a rectangular collection of numbers, a tensor could be a cube of numbers or even some higher-dimensional set of numbers.
You might also have heard that a tensor is something that has upper and lower indices, such as the Riemann tensor above, things that have arcane manipulation rules such as "Einstein summation."
Or you might have heard that a tensor is something that changes coordinates like a tensor. A tensor is as a tensor does. Something that behaves the right way under certain changes of variables is a tensor.
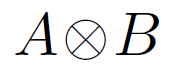
And then there's things that aren't called tensors, but they have tensor products. These seem simple enough in some cases-you think "I didn't realize that has a name. So it's called a tensor product. Good to know." But then in other cases tensor products seem more elusive. If you look in an advanced algebra book hoping for a simple definition of a tensor product, you might be disappointed and feel like the book is being evasive or even poetic because it describes what a tensor product does rather than what it is. That is, the definition is behavioral rather than constructive.
What do all these different uses of the word "tensor" have to do with each other? Do they have anything to do with the TensorFlow machine learning library that Google released recently? That's something I'd like to explore over a series of blog posts.
Next posts in the series: