Visualizing graph spectra like chemical spectra

You can associate a matrix with a graph and find the eigenvalues of that matrix. This gives you a spectrum associated with the graph. This spectrum tells you something about the graph analogous to the way the spectrum of a star's light tells you something about the chemical composition of the start.

So maybe it would be useful to visualize graph spectra the way you visualize chemical spectra. How could you do this?

First, scale the spectrum of the graph to the visual spectrum. There are different kinds of matrices you can associate with a graph, and these have different natural ranges. But if we look at the spectrum of the Laplacian matrix, the eigenvalues are between 0 and n for a graph with n nodes.

Eigenvalues typically correspond to frequencies, not wavelengths, but chemical spectra are often displayed in terms of wave length. We can't be consistent with both, so we'll think of our eigenvalues as wavelengths. We could easily redo everything in terms of frequency.

This means we map 0 to violet (400 nm) and n to red (700 nm). So an eigenvalue of I will be mapped to 400 + 300 I/n. That tells us where to graph a spectral line, but what color should it be? StackOverflow gives an algorithm for converting wavelength to RGB values. Here's a little online calculator based on the same code.

Here are some examples. First we start with a random graph.

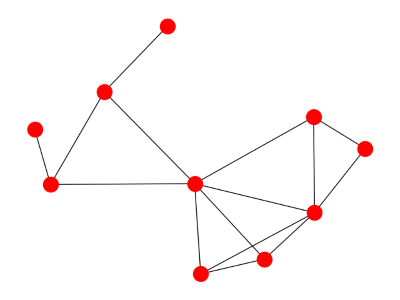
Here's what the spectrum looks like:

Here's a cyclic graph:

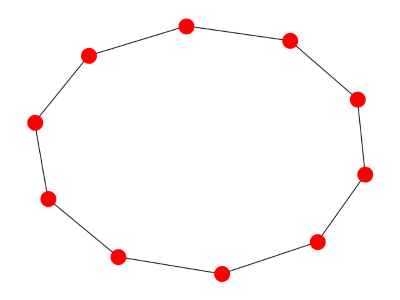
And here's its spectrum:

Finally, here's a star graph:

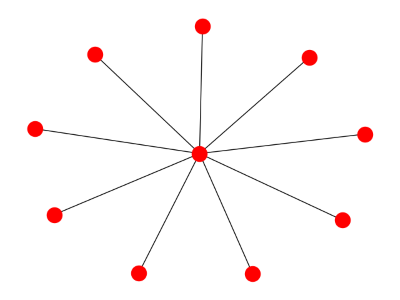
And its spectrum:

Related: Ten spectral graph theory posts