How areas of math are connected
In my previous post, I discussed how number theory and topology relate to other areas of math. Part of that was to show a couple diagrams from Jean Dieudonni(C)'s book Panorama of Pure Mathematics, as seen by N. Bourbaki. That book has only small star-shaped diagrams considering one area of math at a time. I've created a diagram that pastes these local views into one grand diagram. Along the way I've done a little editing because the original diagrams were not entirely consistent.
Here's a condensed view of the graph. You can find the full image here.
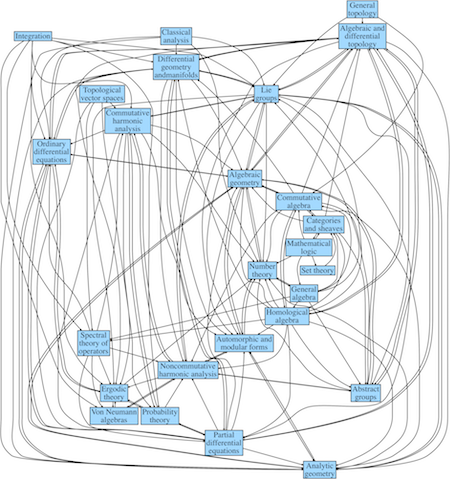
The graph is so dense that it's hard to tell which areas have the most or least connections. Here are some tables to clarify that. First, counting how many areas an particular area contributes to, i.e. number of outgoing arrows.
|-------------------------------------+---------------|| Area | Contributions ||-------------------------------------+---------------|| Homological algebra | 12 || Lie groups | 11 || Algebraic and differential topology | 10 || Categories and sheaves | 9 || Commutative algebra | 9 || Commutative harmonic analysis | 9 || Algebraic geometry | 8 || Differential geometry and manifolds | 8 || Integration | 8 || Partial differential equations | 8 || General algebra | 7 || Noncommutative harmonic analysis | 6 || Ordinary differential equations | 6 || Spectral theory of operators | 6 || Analytic geometry | 5 || Automorphic and modular forms | 5 || Classical analysis | 5 || Mathematical logic | 5 || Abstract groups | 4 || Ergodic theory | 4 || Probability theory | 4 || Topological vector spaces | 4 || General topology | 3 || Number theory | 3 || Von Neumann algebras | 2 || Set theory | 1 ||-------------------------------------+---------------|
Next, counting the sources each area draws on, i.e. counting incoming arrows.
|-------------------------------------+---------|| Area | Sources ||-------------------------------------+---------|| Algebraic geometry | 13 || Number theory | 12 || Lie groups | 11 || Noncommutative harmonic analysis | 11 || Algebraic and differential topology | 10 || Analytic geometry | 10 || Automorphic and modular forms | 10 || Ordinary differential equations | 10 || Ergodic theory | 9 || Partial differential equations | 9 || Abstract groups | 8 || Differential geometry and manifolds | 8 || Commutative algebra | 6 || Commutative harmonic analysis | 6 || Probability theory | 5 || Categories and sheaves | 4 || Homological algebra | 4 || Spectral theory of operators | 4 || Von Neumann algebras | 4 || General algebra | 2 || Mathematical logic | 1 || Set theory | 1 || Classical analysis | 0 || General topology | 0 || Integration | 0 || Topological vector spaces | 0 ||-------------------------------------+---------|
Finally, connectedness, counting incoming and outgoing arrows.
|-------------------------------------+-------------|| Area | Connections ||-------------------------------------+-------------|| Lie groups | 22 || Algebraic geometry | 21 || Algebraic and differential topology | 20 || Noncommutative harmonic analysis | 17 || Partial differential equations | 17 || Differential geometry and manifolds | 16 || Homological algebra | 16 || Ordinary differential equations | 16 || Analytic geometry | 15 || Automorphic and modular forms | 15 || Commutative algebra | 15 || Commutative harmonic analysis | 15 || Number theory | 15 || Categories and sheaves | 13 || Ergodic theory | 13 || Abstract groups | 12 || General algebra | 10 || Spectral theory of operators | 10 || Probability theory | 9 || Integration | 8 || Mathematical logic | 6 || Von Neumann algebras | 6 || Classical analysis | 5 || Topological vector spaces | 4 || General topology | 3 || Set theory | 2 ||-------------------------------------+-------------|
There are some real quirks here. The most foundational areas get short shrift. Set theory contributes to only one area of math?! Topological vector spaces don't depend on anything, not even topology?!
I suspect Dieudonni(C) had in mind fairly high-level contributions. Topological vector spaces, for example, obviously depend on topology, but not deeply. You could do research in the area while seldom drawing on more than an introductory topology course. Elementary logic and set theory are used everywhere, but most mathematicians have no need for advanced logic or set theory.
More math diagrams:
- Diagram of probability distribution relationships
- Modes of convergence
- Topological properties diagram
- Category Relationships in Mathematical Physics
- Category theory definition dependencies
- Conjugate prior diagram
- Topological vector spaces