When length equals area
by John from John D. Cook on (#2PKMG)
The graph of hyperbolic cosine is called a catenary. A catenary has the following curious property: the length of a catenary between two points equals the area under the catenary between those two points.
The proof is surprisingly simple. Start with the following:
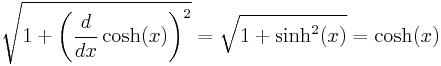
Now integrate the first and last expressions between two points a and b. Note that the former integral gives the arc length of cosh between a and b, and the later integral gives the area under the graph of cosh between a and b.
By the way, the most famous catenary may be the Gateway Arch in St. Louis, Missouri.
