Length of a rose
The polar graph of r = cos(kI) is called a rose. If k is even, the curve will trace out 2k petals as I runs between 0 and 2I. If k is odd, it will trace out k petals, tracing each one twice. For example, here's a rose with k = 5.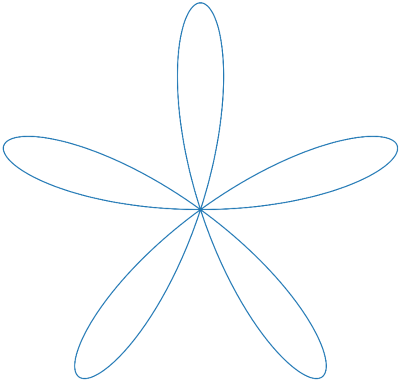
(I rotated the graph 36 so it would be symmetric about the vertical axis rather than the horizontal axis.)
The arc length of a curve in polar coordinates is given by

and so we can use this find the length. The integral doesn't have a closed form in terms of elementary functions. Instead, the result turns out to use a special function E(x), the "complete elliptic integral of the second kind," defined by

Here's the calculation for the length of a rose:

So the arc length of the rose r = cos(kI) with I running from 0 to 2I is 4 E(-k^2 + 1). You can calculate E in SciPy with scipy.special.ellipe.
If we compute the length of the rose at the top of the post, we get 4 E(-24) = 21.01. Does that pass the sniff test? Each petal goes from r = 0 out to r = 1 and back. If the petal were a straight line, this would have length 2. Since the petals are curved, the length of each is a little more than 2. There are five petals, so the result should be a little more than 10. But we got a little more than 20. How can that be? Since 5 is odd, the rose with k = 5 traces each petal twice, so we should expect a value of a little more than 20, which is what we got.
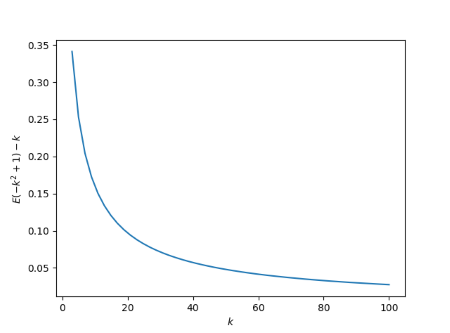
As k gets larger, the petals come closer to being straight lines. So we should expect that 4E(-k^2 + 1) approaches 4k as k gets large. The following plot of E(-k^2 + 1) - k provides empirical support for this conjecture by showing that the difference approaches 0, and gives an idea of the rate of convergence. It should be possible to prove that, say, that E(-k^2) asymptotically approaches k, but I haven't done this.
Related posts: