Least common multiple of the first n positive integers

Here's a surprising result: The least common multiple of the first n positive integers is approximately exp(n).

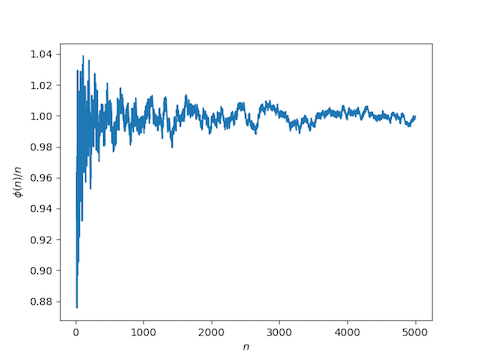
More precisely, let I(n) equal the log of the least common multiple of the numbers 1, 2, ", n. There are theorems that give upper and lower bounds on how far I(n) can be from n. We won't prove or even state these bounds here. See [1] for that. Instead, we'll show empirically that I(n) is approximately n.

Here's some Python code to plot I(n) over n. The ratio jumps up sharply after the first few values of n. In the plot below, we chop off the first 20 values of n.

from scipy import arange, emptyfrom sympy.core.numbers import ilcmfrom sympy import logimport matplotlib.pyplot as pltN = 5000x = arange(N)phi = empty(N)M = 1for n in range(1, N): M = ilcm(n, M) phi[n] = log(M)a = 20plt.plot(x[a:], phi[a:]/x[a:])plt.xlabel("$n$")plt.ylabel("$\phi(n) / n$")plt.show()

Here's the graph this produces.

[1] J. Barkley Rosser and Lowell Schoenfeld. Approximate formulas for some functions of prime numbers. Illinois Journal of Mathematics, Volume 6, Issue 1 (1962), 64-94. (On Project Euclid)