The chaos game and the Sierpinski triangle

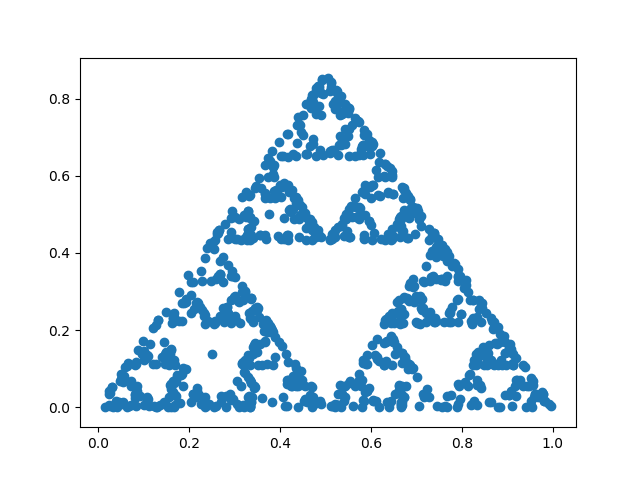
The chaos game is played as follows. Pick a starting point at random. Then at each subsequent step, pick a triangle vertex at random and move half way from the current position to that vertex.

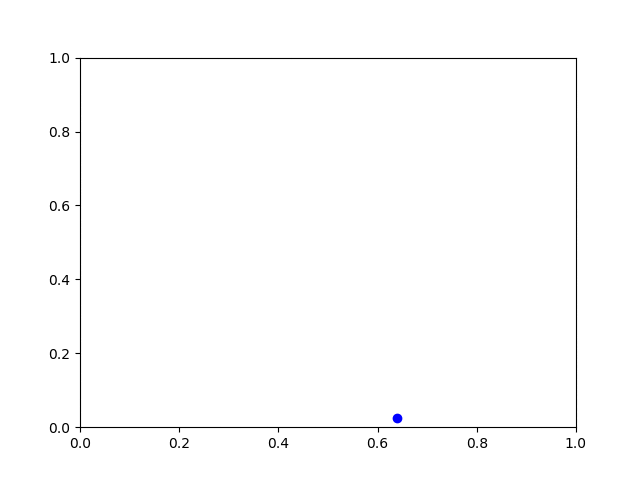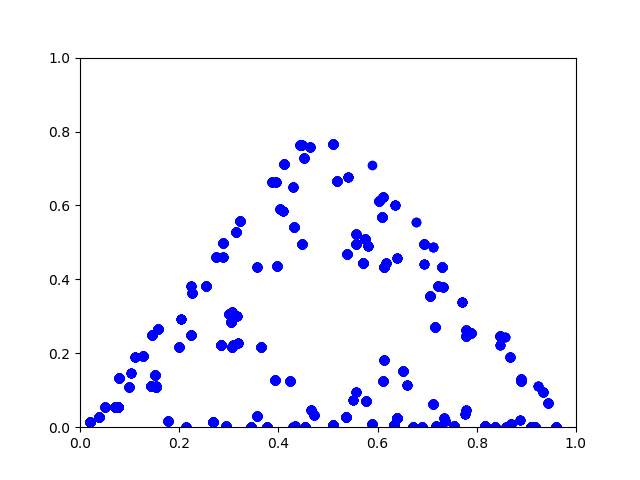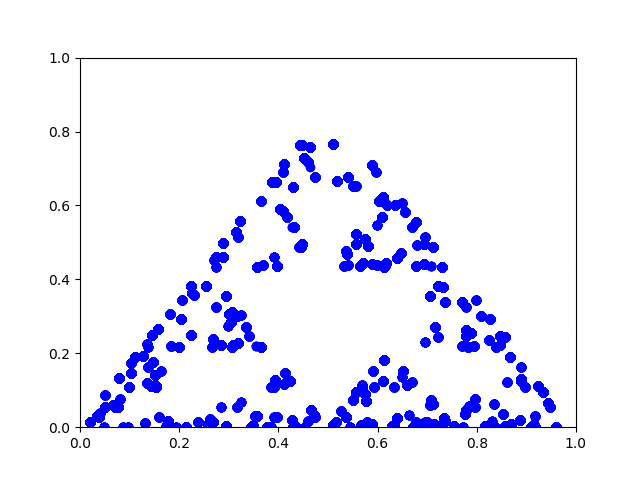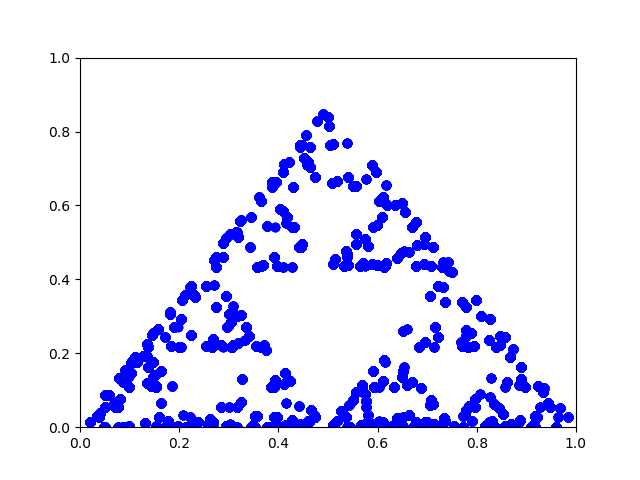
The result looks like a fractal called the Sierpinski triangle or Sierpinski gasket.

Here's an example:

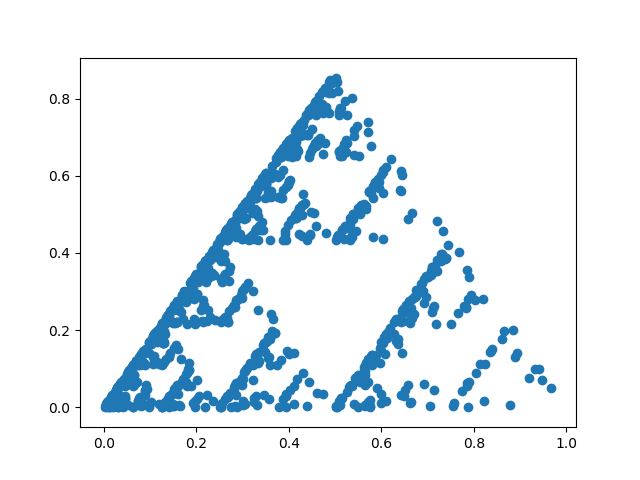
If the random number generation is biased, the resulting triangle will show it. In the image below, the lower left corner was chosen with probability 1/2, the top with probability 1/3, and the right corner with probability 1/6.

Update: Here's an animated version that lets you watch the process in action.

Here's Python code to play the chaos game yourself.

from scipy import sqrt, zerosimport matplotlib.pyplot as pltfrom random import random, randintdef midpoint(p, q): return (0.5*(p[0] + q[0]), 0.5*(p[1] + q[1]))# Three corners of an equilateral trianglecorner = [(0, 0), (0.5, sqrt(3)/2), (1, 0)]N = 1000x = zeros(N)y = zeros(N)x[0] = random()y[0] = random()for i in range(1, N): k = randint(0, 2) # random triangle vertex x[i], y[i] = midpoint( corner[k], (x[i-1], y[i-1]) ) plt.scatter(x, y)plt.show()

Update 2: Peter Norvig posted some Python code with variations on the game presented here, generalizing a triangle to other shapes. If you try the analogous procedure with a square, you simply get a square filled with random dots.

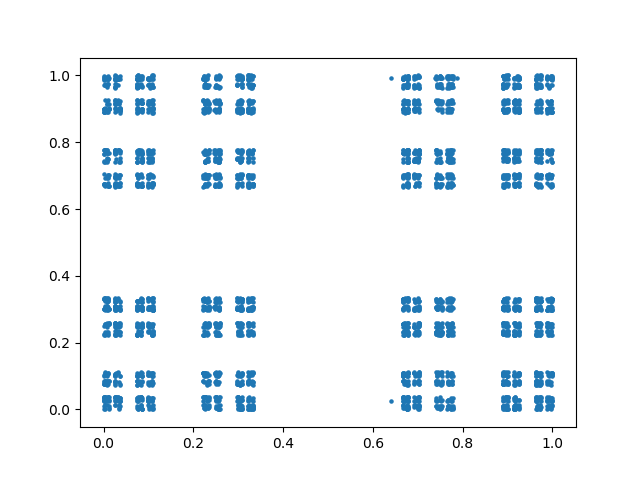
However, you can get what you might expect, the square analog of the Sierpinski triangle, the product of a Cantor set with itself, if you make a couple modifications. First, pick a side at random, not a corner. Second, move 1/3 of the way toward the chosen side, not 1/2 way.

Here's what I got with these changes:

Source: Chaos and Fractals