No critical point between two peaks

If a function of one variable has two local maxima, it must have a local minimum in between.

What about a function of two variables? If it has two local maxima, does it need to have a local minimum? No, it could have a saddle point in between, a point that is a local minimum in one direction but a local maximum in another direction. But even more surprising, it need not even have a saddle point. A function of two variables could have two local maxima and no other critical points! Here's an example:

f(x, y) = - (x^2 - 1)^2 - (x^2y - x - 1)^2

It's clear that the function is zero at (-1, 0) and (1, 2), and that the function is negative otherwise. So it clearly has two local maxima. You can write out the partial derivatives with respect to x and y and see that the only place they're both zero is at the two local maxima.

Here's a plot of the function:

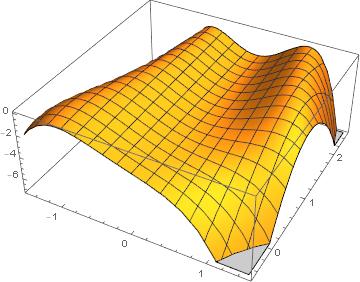
And here's a contour plot:

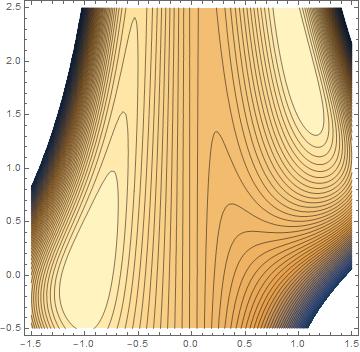
The two maxima are in in the bright patches in the lower left and upper right.

You might be thinking that if you walk between two peaks, you've got to go down in between. And that's true. If you walk in a straight line between (-1, 0) and (1, 2), you'll run into a local minimum around (0.2316, 1.2316). But that's only a local minimum along your path. It's not a local minimum or saddle point of the function in a neighborhood of that point.

I found this example in the book Single Digits.