Recent exponential sums

The exponential sum of the day draws a line between consecutive partial sums of

where m, d, and y are the current month, day, and two-digit year. The four most recent images show how different these plots can be.

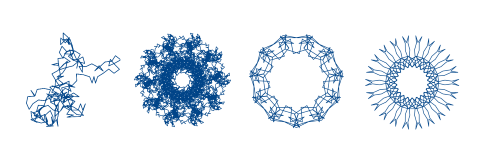
These images are from 10/30/17, 10/31/17, 11/1/17, and 11/2/17.

Consecutive dates often produce very different images for a couple reasons. First, consecutive integers are relatively prime. From a number theoretic perspective, 30 and 31 are very different, for example. (This touches on the motivation for p-adic numbers: put a different metric on integers, one based on their prime factorization.)

The other reason consecutive dates produce qualitatively different images is that you might roll over a month or year, such as going from October (10) to November (11). You'll see a big change when we roll over from 2017 to 2018.

The partial sums are periodic with period lcm(m, d, y). The image for 10/31/17 above has the most points because 10, 31, and 17 are relatively prime. It's also true that 11, 2, and 17 are relatively prime, but these are smaller numbers.

You could think of the month, day, and year components of the sum as three different gears. The sums repeat when all three gears return to their initial positions. In the image for yesterday, 11/1/17, the middle gear is effectively not there.