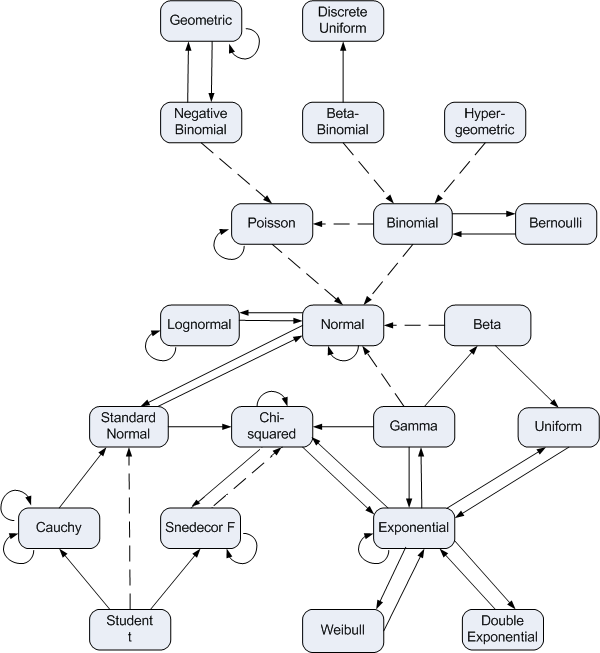
Quantifying normal approximation accuracy

John

from John D. Cook on 2018-02-19 15:29 (#3G8KD)

Probability is full of theorems that say that probability density approximates another as some parameter becomes large. All the dashed lines in the diagram below indicate a relationship like this.

You can find details of what everything in the diagram means here.

How can you quantify these approximations? One way is to use Kullback-Leibler divergence. In this post I'll illustrate this for the normal approximation to the beta and gamma distributions.

The Kullback-Leibler divergence between two random variables X and Y is defined as

We will compute this integral numerically in the code below to create graphs of how K-L divergence varies with parameters.

Here are the imports we'll need.

 from scipy.integrate import quad from scipy.stats import beta, gamma, norm from scipy import inf import matplotlib.pyplot as plt

Beta distribution

As the shape parameters of a beta distribution become large, the probability distribution becomes approximately normal (Gaussian).

Here is code that will take the two shape parameters of a beta distribution, construct a normal approximation by moment matching, and compute the quality of the approximation as measured by Kullback-Leibler divergence.

 def KL_beta_norm(a, b): b = beta(a, b) n = norm(b.mean(), b.std()) f = lambda x: -b.pdf(x)*(n.logpdf(x) - b.logpdf(x)) integral, error = quad(f, 0, 1) return integral

And here we make our plot.

 x = [2**i for i in range(11)] y = [KL_beta_norm(t, 2*t) for t in x] plt.plot(x, y) plt.xscale("log") plt.yscale("log") plt.xlabel("a") plt.ylabel("KL divergence") plt.title("Comparing beta(a, 2a) and its normal approximation") plt.savefig("beta_KL.svg") plt.close()

The result is nearly linear on a log-log scale.

I made the b parameter twice the a parameter to show that you don't need symmetry. When you do have symmetry, i.e a = b, the approximation quality is better and the graph is even straighter.

Gamma distribution

As the shape parameter of a gamma distribution increases, the probability density becomes more and more like that of a normal distribution. We can quantify this with the following code.

 def KL_gamma_norm(shape): g = gamma(shape) n = norm(g.mean(), g.std()) f = lambda x: -g.pdf(x)*(n.logpdf(x) - g.logpdf(x)) mode = max(0, shape-1) integral1, error1 = quad(f, 0, mode) integral2, error2 = quad(f, mode, inf) return integral1 + integral2

The integration code is a little more complicated this time. For small shape parameters, code analogous to that for the beta distribution will work just fine. But for larger parameters, the integration fails. The numerical integration routine needs a little help. The largest contribution to the integral is located near the mode of the gamma distribution. For large shape parameters, the integration routine misses this peak and grossly underestimates the integral. We break the integral into two pieces at the mode of the gamma distribution so the integration routine can't miss it. This is a small example of why numerical integration cannot be completely automated. You have to know something about what you're integrating.

(The quad() function has a parameter points to let you tell it about points of interest like this, but it doesn't work when one of the limits of integration is infinite.)

The plotting code is essentially the same as that for the beta distribution. As before, the plot is linear on a log-log scale.

You could do a similar analysis on the other approximations in the distribution relationship diagram above.

Source	RSS or Atom Feed
Feed Location	http://feeds.feedburner.com/TheEndeavour?format=xml
Feed Title	John D. Cook
Feed Link	https://www.johndcook.com/blog