Redoing division algebra graphs with angular distance
The blog post that kicked off the recent series of posts looked at how far apart xy and yx are for quaternions. There I used the Euclidean distance, i.e. || xy - yx ||. This time I'll look at the angle between xy and yx, and I'll make some analogous graphs for octonions.
For vectors x and y in three dimensions, the dot product satisfies
where I is the angle between the two vectors. In higher dimensions, we can turn this theorem around and use it as the definition of the angle between two vectors based on their dot product.
(The plots below are jagged because they're based on random sampling.)
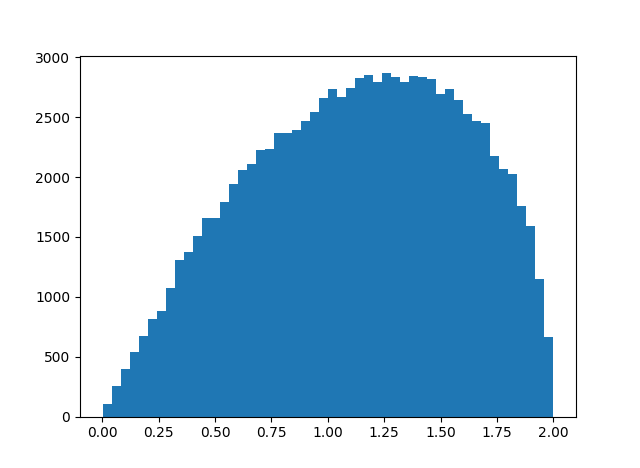
Here's the Euclidean distance between xy and yx for quaternions from the earlier post:
And here's the corresponding angular distance:
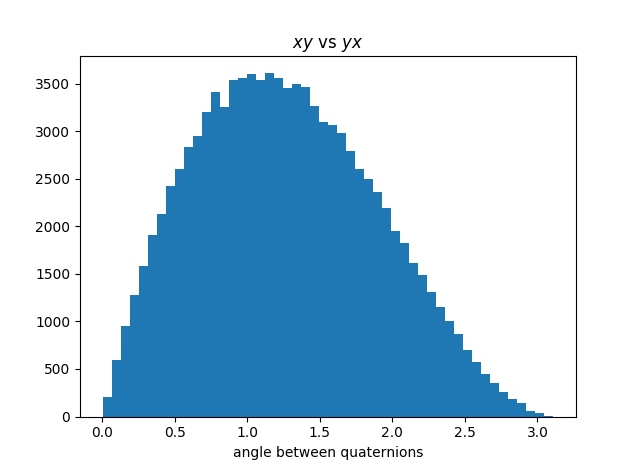
The range has changed from [0, 2] to [o, I], and the distribution now shifts left instead of right.
Here's a similar graph, looking at the angular distance between xy and yx for octonions, something I haven't plotted before in Euclidean distance.
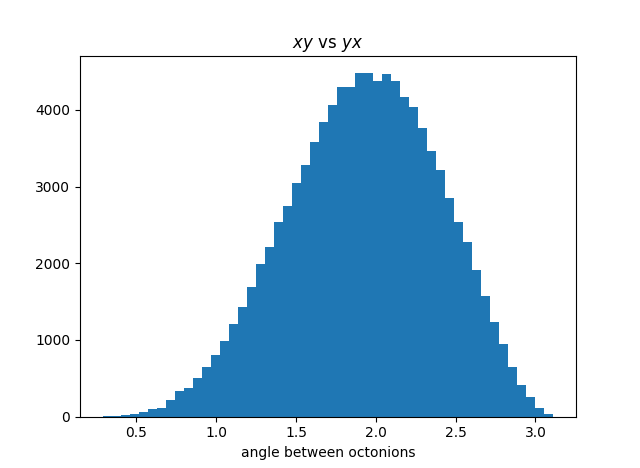
This graph is more symmetric, which we might expect: since octonions have less algebraic structure than quaternions, we might expect the relationship between xy and yz to behave more erratically, and for the plot to look more like a normal distribution.
Finally, let's revisit the distance between (xy)z and x(yz) for octonions. Here is the distribution of the Euclidean distance from a previous post:
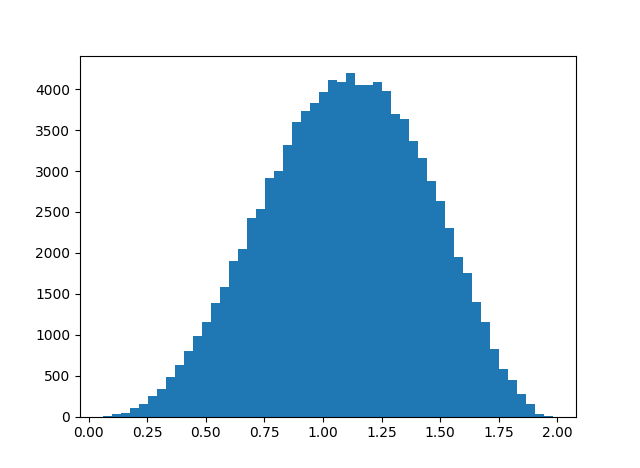
And here is the corresponding histogram based on angular distance.
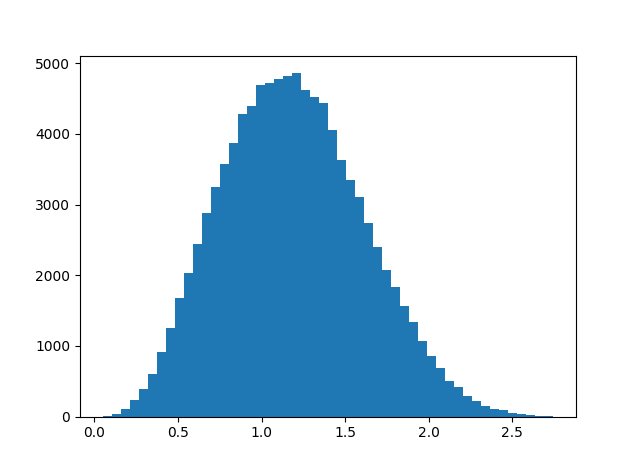
These plots are based on uniform random samples of quaternions and octonions of length 1, i.e. points from the unit spheres in 4 and 8 dimensions respectively. Quaternions and octonions have the property that the product of unit length vectors is another unit length vector, and the angle between to unit vectors is the inverse cosine of their dot product.
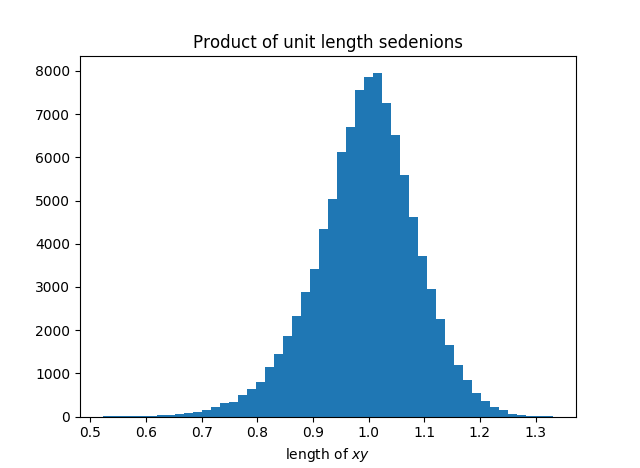
I thought that sedenions also had this norm property, that the product of unit length vectors has unit length. Apparently not, as I discovered by trying to take the inverse cosine of a number larger than 1. So what is the distribution of lengths that come from multiplying two sedenions of length 1? Apparently the mean is near 1, and here's a histogram.