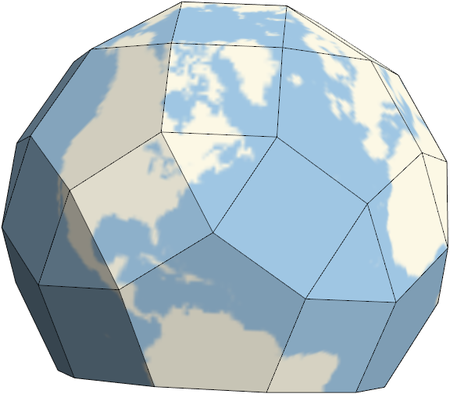
Projecting the globe onto regular solids
I was playing around with some geographic features of Mathematica this morning and ran across an interesting example in the documentation for the PolyhedronProjection function given here. Here's what you get when you project a map of the earth onto each of the five regular (Platonic) solids.
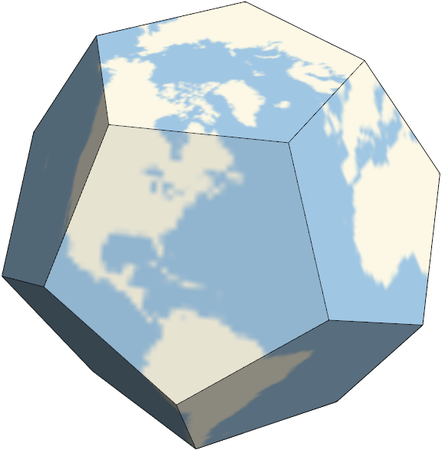
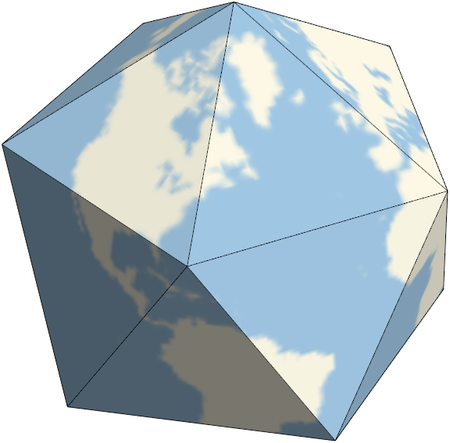

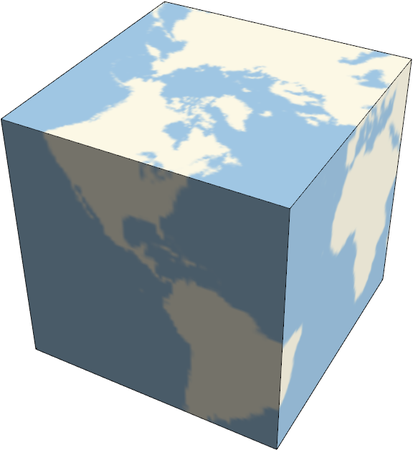

At first I right-clicked on each image and saved as graphic files. This produced low quality images, even when I saved as SVG. I got better resolution by using the Export command and specifying the ImageSize and ImageResolution options.
The default view of the tetrahedron was face-on, so it looked like a flat triangle. By changing the ViewPoint I was able to get something that's more clearly three dimensional.
By the way, you can use PolyhedronProjection to project onto more exotic polyhedra than the Platonic solids. For example,
Export["rhomb.png", PolyhedronProjection["ParagyrateDiminishedRhombicosidodecahedron"], ImageResolution -> 72, ImageSize -> Large]
produces this: