Extremely small probabilities
One objection to modeling adult heights with a normal distribution is that the former is obviously positive but the latter can be negative. However, by this model negative heights are astronomically unlikely. I'll explain below how one can take "astronomically" literally in this context.
A common model says that men's and women's heights are normally distributed with means of 70 and 64 inches respectively, both with a standard deviation of 3 inches. A woman with negative height would be 21.33 standard deviations below the mean, and a man with negative height would be 23.33 standard deviations below the mean. These events have probability 3 i- 10-101 and 10-120 respectively. Or to write them out in full
0.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000003
and
0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001.
As I mentioned on Twitter yesterday, if you're worried about probabilities that require scientific notation to write down, you've probably exceeded the resolution of your model. I imagine most probability models are good to two or three decimal places at most. When model probabilities are extremely small, factors outside the model become more important than ones inside.
According to Wolfram Alpha, there are around 1080 atoms in the universe. So picking one particular atom at random from all atoms in the universe would be on the order of a billion trillion times more likely than running into a woman with negative height. Of course negative heights are not just unlikely, they're impossible. As you travel from the mean out into the tails, the first problem you encounter with the normal approximation is not that the probability of negative heights is over-estimated, but that the probability of extremely short and extremely tall people is under-estimated. There exist people whose heights would be impossibly unlikely according to this normal approximation. See examples here.
Probabilities such as those above have no practical value, but it's interesting to see how you'd compute them anyway. You could find the probability of a man having negative height by typing pnorm(-23.33) into R or scipy.stats.norm.cdf(-23.33) into Python. Without relying on such software, you could use the bounds
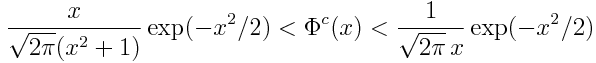
with x equal to -21.33 and -23.33. For a proof of these bounds and tighter bounds see these notes.