Self-curvature
If you look at a sine wave, its curvature is sorta like its values. When sine is zero, the curve is essentially a straight line, and the curvature is zero. When sine is at its maximum, the function bends the most and so the curvature is at a maximum.
This makes sense analytically. The second derivative is something like curvature, and the second derivative of sin(x) is -sin(x). The negative sign suggests that if we look at signed curvature rather than absolute curvature, then the values of a sine curve are roughly proportional to the negative of the curvature at each point.
Here's a plot showing sin(x) and its negative curvature.
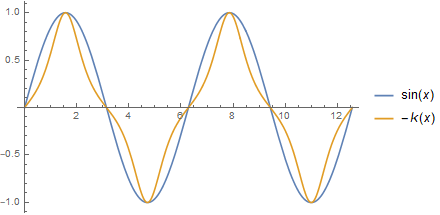
Steven Wilkinson wrote an article [1] addressing the question of whether there is a curve so that the curvature at each point is proportional to the value of the curve. The curvature of a graph of y = y(x) is
and so a curve that is proportional to its curvature is a solution to the nonlinear differential equation
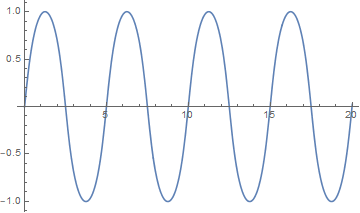
General theory says that there should at least be a solution in a (possibly small) neighborhood of 0, but it's not obvious a priori that interesting solutions exist. It turns out that if we pick the proportionality constant a = -1 and the initial conditions y(0) = 0 and y '(0) = a3 then we get a periodic solution that looks something like a sine.
The following Mathematica code will plot the function for us.
s = NDSolve[ {y''[x] = -y[x] (1 + y'[x]^2)^(-3/2), y[0] == 0, y'[0] == Sqrt[3]}, y, {x, 0, 10}] Plot[Evaluate[{y[x] /. s}], {x, 0, 10}]The plot looks a lot like a sine wave. In fact, I imagine that when asked to draw a sine wave, most people would draw something that looks more like this than like an actual sine wave.
[1] Steven Wilkison. Self-Curvature Curves. Mathematics Magazine, Vol. 82, No. 5 (December 2009), pp. 354-359