Near zeros of zeta

Alex Kontorovich had an interesting tweet about the Riemann hypothesis a few days ago.

Why is the Riemann Hypothesis hard? Just one reason (of very many): it's not an analytic question. Here are the values of zeta on the 1/2-line (where at least 40% of the zeros are, all should be) and the 4/5-line, where none should be. The latter gets arbitrarily close to 0, i.o. pic.twitter.com/qSHhwwCY6X

- Alex Kontorovich (@AlexKontorovich) November 25, 2019

The critical strip of the Riemann zeta function is the portion of the complex plane with real part between 0 and 1. The Riemann hypothesis conjectures that the zeros of the zeta function in this region all have real part 1/2. To put it another way, the Riemann hypothesis says that I(x + it) is never zero unless x = 1/2. However, according to Alex Kontorovich's tweet, the function gets arbitrarily close to zero infinitely often for other values of x.

I wrote a little Mathematica code to produce graphs like the ones above. Here is a plot of I(1/2 + it).

 ParametricPlot[ {Re[Zeta[1/2 + I t]], Im[Zeta[1/2 + I t]]}, {t, 0, 100}, AspectRatio -> 1, PlotRange -> {{-2, 6}, {-3, 3}} ]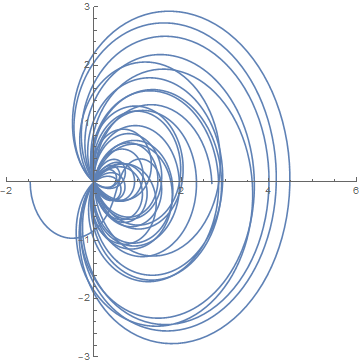

At first I didn't specify the aspect ratio and I got nearly circular arcs. Then I realized that was an artifact of Mathematica's default aspect ratio. Also, I set the plot range so the image above would be comparable with the next image.

Notice all the lines crossing the origin. These correspond to the zeros of I along the line Re(x) = 1/2.

Next I changed the 1/2 to 1/3.

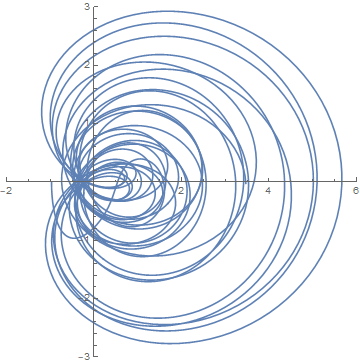
If you look closely you'll see a gap around the origin.

Here's a closeup of the origin in both graphs. First for x = 1/2

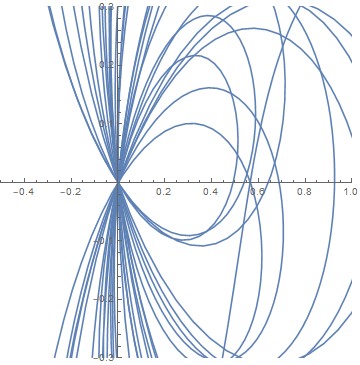
and now for x = 1/3.

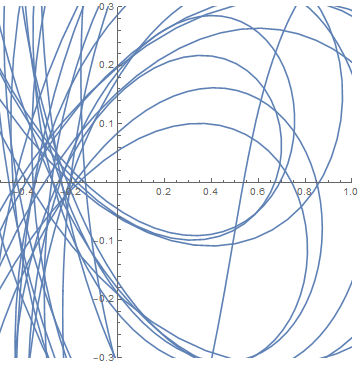
I hadn't seen the result in Kontorovich's tweet before. I don't know whether it holds for all x or just for certain values of x. I assume the former. But apparently it at least holds for x = 4/5. So we should be able to find values of |&zeta(4/5 + it)| as small as we like by taking t large enough, and we should always be able to find more such values by looking further out. In practice, you might have to very far out before you find a small value. Looking as far as 1000, for example, it seems the minimum is about 0.2.

 Plot[ Abs[Zeta[4/5 + I t]], {t, 0, 1000}, PlotRange -> {0, 1} ]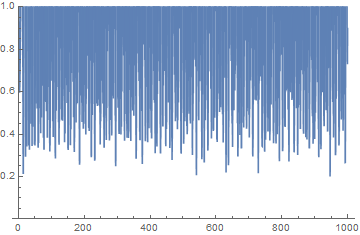

If you ask Mathematica to find the minimum in the graph above, it won't give a reasonable answer; there are too many local minima. If instead you ask it to look repeatedly over small intervals, it does much better. The following minimizes |I(4/5 + it)| over the interval [i, i+1].

 f[i_] := FindMinimum[ {Abs[Zeta[4/5 + I t]], i 

It returns a pair: the minimum and where it occurred. The following will look for places where |I(4/5 + it)| is less than 0.2.

 For[i = 0, i 

It finds two such values.

{0.191185, {t->946.928}}{0.195542, {t->947.}}

As I write this I have a longer program running, and so far the smallest value I've found is 0.1809 which occurs at t = 1329.13. According to Kontorovich you can find as small a value as you like, say less than 0.1 or 0.001, but apparently it might take a very long time.

Update: The minimum over 0 a t a 10,000 is 0.142734, which occurs at 7563.56.

• Distribution of the zeros of I
• Bernoulli numbers, Riemann zeta, and strange sums
• Probability of coprime sets