Behold! The Brusselator!
Having watched a few episodes of Phineas and Ferb, when I see "Brusselator" I imagine Dr. Doofenschmertz saying "Behold! The Brusselator!"
But the Brusselator is considerably older than Phineas and Ferb. It goes back to Belgian scientists Reni(C) Lefever and Gri(C)goire Nicolis in 1971 [1] who combined "Brussels" and "oscillator" to name the system after their institution, Universiti(C) Libre de Bruxelles. It's a dynamical system that has its origins in modeling chemical reactions.
The phase plot below shows that as you start from multiple initial conditions, you always end up on the same limit cycle.
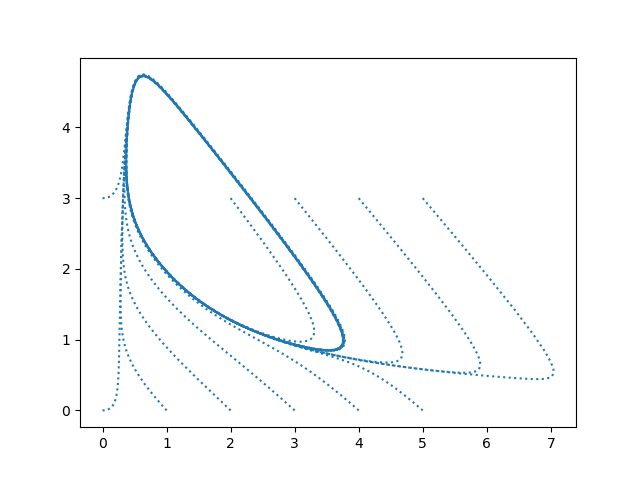
Here's the Python code that produced the plot.
from scipy import linspace from scipy.integrate import solve_ivp import matplotlib.pyplot as plt A, B = 1, 3 def brusselator(t, z): x, y = z return [A + x*x*y - (B+1)*x, B*x - x*x*y] a, b = 0, 10 t = linspace(a, b, 1000) for x0 in range(0, 6): for y0 in [0, 3]: sol = solve_ivp(brusselator, [a, b], [x0, y0], t_eval=t) plt.plot(sol.y[0], sol.y[1], ":", color="tab:blue") plt.show()More dynamical systems posts
[1] R. Lefever and G. Nicholis. Chemical instabilities and sustained oscillations. Journal of Theoretical Biology. Volume 30, Issue 2, February 1971, Pages 267-284