A tale of two iterations
I recently stumbled on a paper [1] that looks at a cubic equation that comes out of a problem in orbital mechanics:
Ifx^3 = (1 + x)^2
Much of the paper is about the derivation of the equation, but here I'd like to focus on a small part of the paper where the author looks at two ways to go about solving this equation by looking for a fixed point.
If you wanted to isolate x on the left side, you could divide by If and get
x = ((x + 1)^2 / If)1/3.
If you work in the opposite direction, you could start by taking the square root of both sides and get
x = a(Ifx3) - 1.
Both suggest starting with some guess at x and iterating. There is a unique solution for any If > 4 and so for our example we'll fix If = 5.
We define two functions to iterate, one for each approach above.
sigma = 5 x0 = 0.1 def f1(x): return sigma**(-1/3)*(x+1)**(2/3) def f2(x): return (sigma*x**3)*0.5 - 1
Here's what we get when we use the cobweb plot code from another post.
cobweb(f1, x0, 10, "ccube1.png", 0, 1.2)
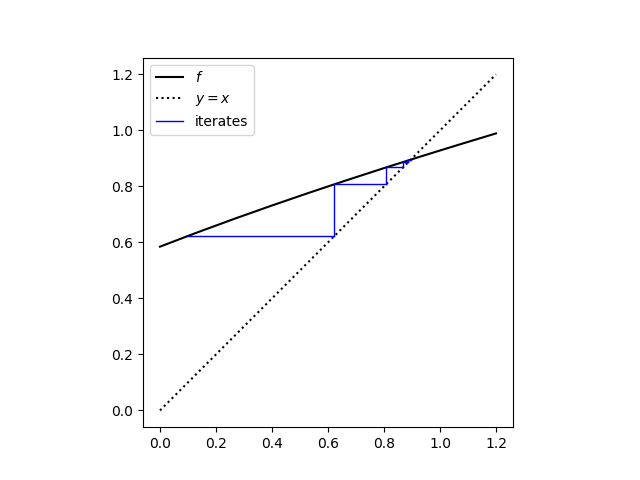
This shows that iterations converge quickly to the solution x = 0.89578.
Now let's try the same thing for f2. When we run
cobweb(f2, x0, 10, "ccube2.png", 0, 1.2)
we get an error message
OverflowError: (34, 'Result too large')
Let's print out a few values to see what's going on.
x = 0.1 for _ in range(10): x = f2(x) print(x)
This produces
-0.9975 -3.4812968359375005 -106.4783129145318 -3018030.585561691 -6.87243939752166e+19 -8.114705541507359e+59 -1.3358518746543001e+180
before aborting with an overflow error. Well, that escalated quickly.
The first iteration converges to the solution for any initial starting point in (0, 1). But the solution is a point of repulsion for the second iteration.
If we started exactly on the solution, the unstable iteration wouldn't move. But if we start as close to the solution as a computer can represent, the iterations still diverge quickly. When I changed the starting point to 0.895781791526322, the correct root to full floating point precision, the script crashed with an overflow error after 9 iterations.
More on fixed points[1] C. W. Groetsch. A Celestial Cubic. Mathematics Magazine, Vol. 74, No. 2 (Apr., 2001), pp. 145-152.