Sine series for a sine

The Fourier series of an odd function only has sine terms-all the cosine coefficients are zero-and so the Fourier series is a sine series.

What is the sine series for a sine function? If the frequency is an integer, then the sine series is just the function itself. For example, the sine series for sin(5x) is just sin(5x). But what if the frequency is not an integer?

For an odd function f on [-I, I] we have

where the coefficients are given by

So if I is not an integer, the sine series coefficients for sin(Ix) are given by

The series converges slowly since the coefficients are O(1/n).

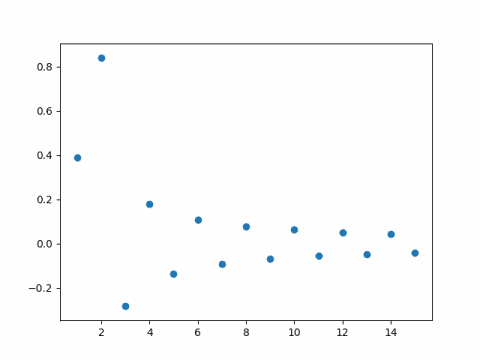
For example, here are the first 15 coefficients for the sine series for sin(1.6x).

And here is the corresponding plot for sin(2.9x).

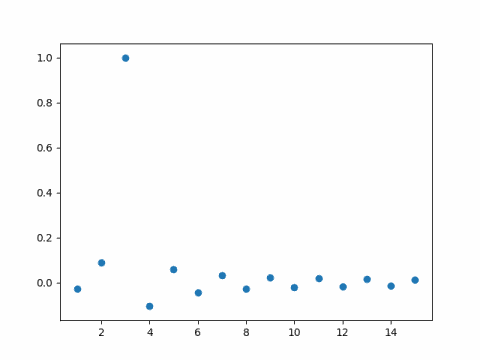
As you might expect, the coefficient of sin(3x) is nearly 1, because 2.9 is nearly 3. What you might not expect is that the remaining coefficients are fairly large.

More posts on Fourier series

• Relating Fourier series and Fourier transforms
• Fourier series for Jacobi functions
• Fourier-Bessel series and Gibbs effect