Negative space graph
Here is a plot of the first 30 Chebyshev polynomials. Notice the interesting patterns in the white space.
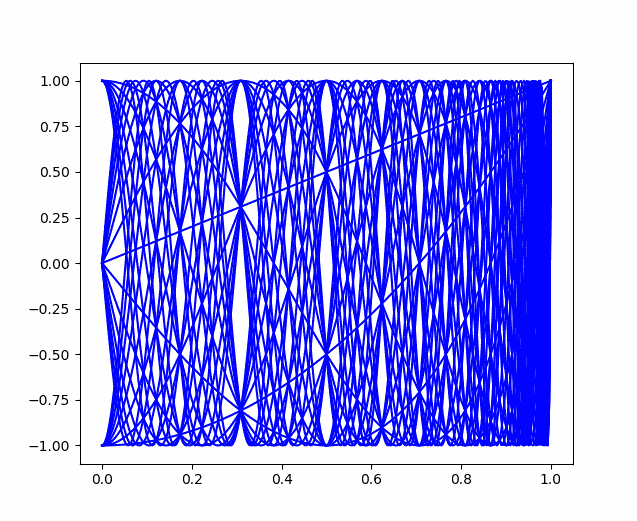
Forman Acton famously described Chebyshev polynomials as cosine curves with a somewhat disturbed horizontal scale." However, plotting cosines with frequencies 1 to 30 gives you pretty much a solid square. Something about the way Chebyshev polynomials disturb the horizontal scale creates the interesting pattern in negative space. (The distortion is different for each polynomial; otherwise the cosine picture would be a rescaling of the Chebyshev picture.)
I found the example above in a book that referenced a book by Theodore Rivlin. There's a new edition of Rivlin's book coming out in August, so maybe it will say something about the gaps.
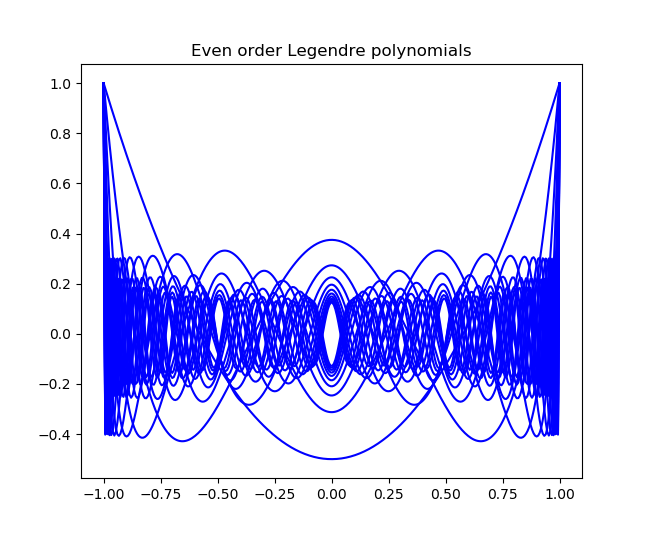
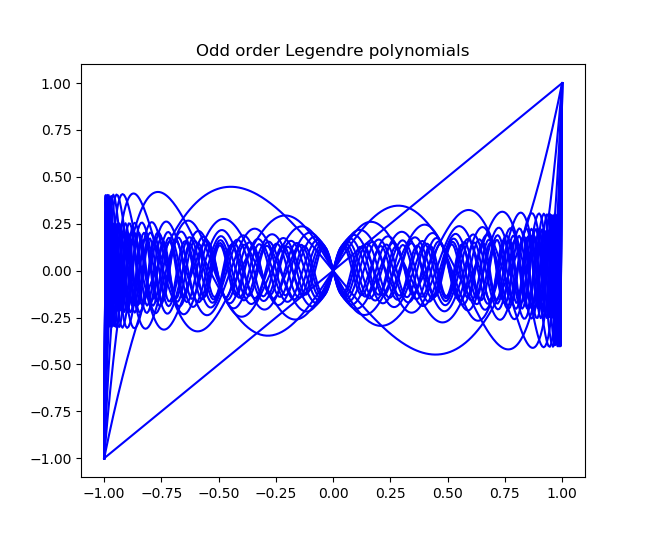
Update: Here are analogous graphs for Legendre polynomials, plotting the even and odd ordered polynomials separately. They also have conspicuous holes, but they don't fill the unit square the way Chebyshev polynomials do.