Five places the Sierpiński triangle shows up

The Sierpiski triangle is a fractal that comes up in unexpected places. I'm not that interested in fractals, and yet I've mentioned the Sierpiski triangle many times on this blog just because I run into it while looking at something else.

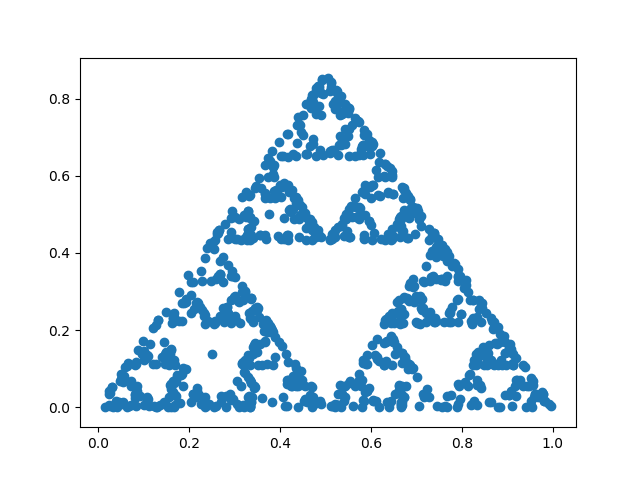
The first time I wrote about the Sierpiski triangle was when it came up in the context of a simple random process called the chaos game.

Next I ran into Sierpiski in the context of cellular automata, specifically Rule 90. A particular initial condition for this rule leads to the image below. With other initial conditions you don't get such a clean Sierpiski triangle, but you do get similar variations on the theme.

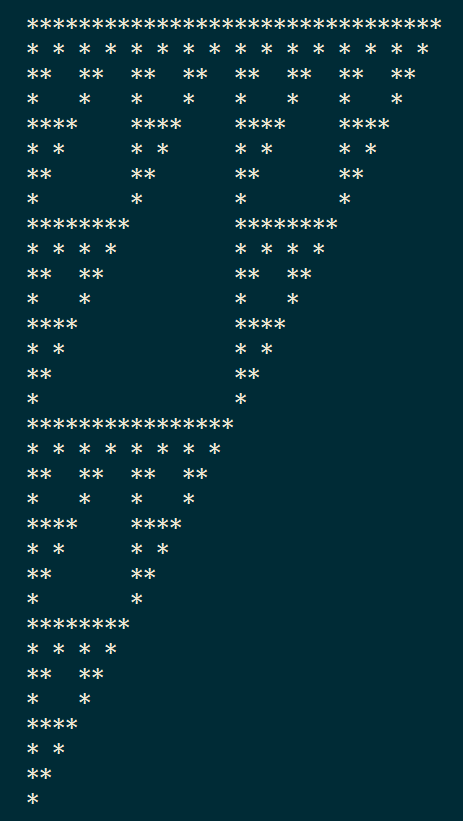
Next I ran into Sierpiski in the context of low-level programming. The following lines of C code prints an asterisk when the bit-wise and of two numbers is non-zero.

 for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) printf("%c", (i&j) ? ' ' : '*'); printf("\n"); }

A screenshot of the output shows our familiar triangle.

Then later I wrote a post looking at constructible n-gons, n-sided figures that can be constructed using only a straight edge and a compass. These only exist for special values of n. If you write these special values in binary, and replace the 1's with a black square and the 0's with a blank, you get yet another Sierpiski triangle.

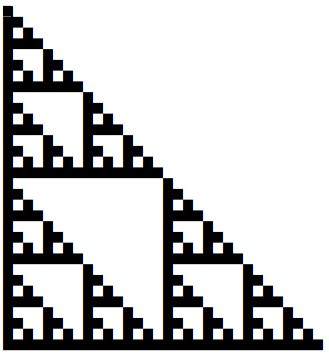
Finally, if you look at the odd numbers in Pascal's triangle, they also form a Sierpiski triangle.