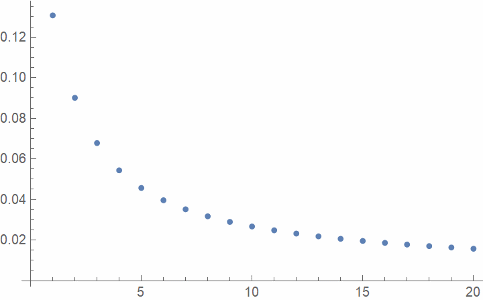Cosine power approximation to normal

Ten years ago I wrote about how cosine makes a decent approximation to the normal (Gaussian) probability density. It turns out you get a much better approximation if you raise cosine to a power.

If we normalize cos^k(t) by dividing by its integral

we get an approximation to the density function for a normal distribution with mean 0 and variance 1/k.

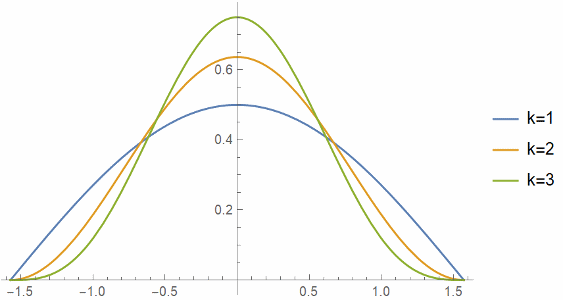
Here are the plots of cos^k(t), normalized to integrate to 1, for k = 1, 2, and 3.

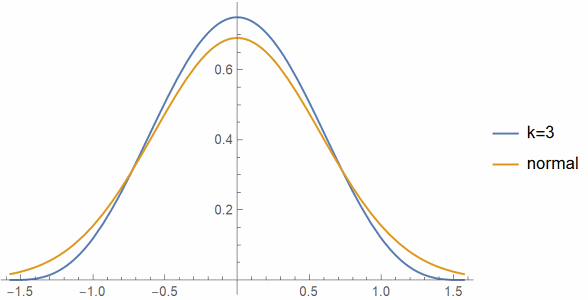
And here's a plot of cos³(t) compared to a normal with variance 1/3.

And finally here's a plot of L^2 error, the square root of the integral of the square of the approximation error, as a function of k.