Life, part 26

Last time on FAIC we saw how we could start with nine 2-quads - a 12*12 grid of cells - and with only a handful of ands, ors and table lookups we could get an 8*8 grid of cells of the next state out. How is that useful?

In order to explain, we need two more data structures, and it should come as no surprise that they are Quad3 and Quad4. Quad3, as I mentioned last time, is trivial; it is just a struct wrapping four Quad2s. The implementation is simpler than Quad2:

struct Quad3{ public Quad3(Quad2 nw, Quad2 ne, Quad2 sw, Quad2 se) { NW = nw; NE = ne; SW = sw; SE = se; } public Quad2 NW { get; } public Quad2 NE { get; } public Quad2 SW { get; } public Quad2 SE { get; } public bool Get(int x, int y) { ... } public Quad3 Set(int x, int y) { ... } public Quad3 Clear(int x, int y) { ... } public override string ToString() { ... }}

We have yet another immutable struct. It's small - only 64 bits. The Get, Set, Clear and ToString implementations are the obvious and straightforward extensions of the similar methods I already showed for Quad2, so I won't bother showing them here. In a few episodes we will need to add some helper methods to Quad3, but for now, this will do us just fine.

The interesting data structure is Quad4, which by rights should represent a 16*16 grid of cells. The Quad4 has some surprises:

• A Quad4 is a mutable class, not an immutable struct.
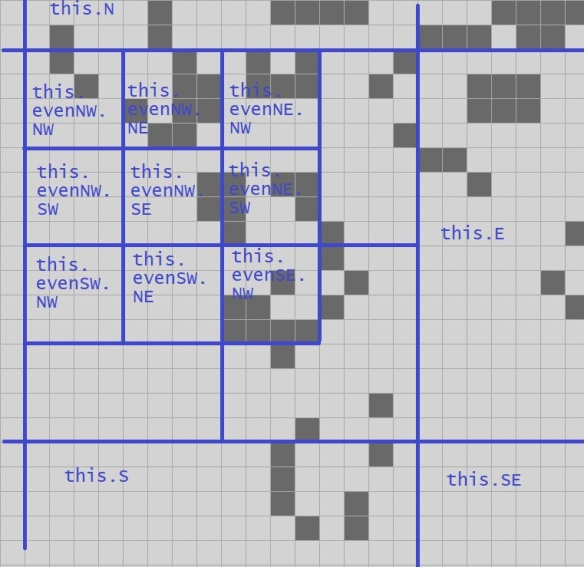
• A Quad4 is not four Quad3s. It is eight! A Quad4 represents two ticks worth of a 16*16 portion of the grid. We have four Quad3s for the even-numbered generations, and four for the odds.
• Each Quad4 is numbered with a unique (x, y) pair of signed short integers. That gives us a square of Quad4s 65536 on a side; since each Quad4 is 16 cells wide and tall, we have a total grid size of just over one million cells on a side; that's a 20-quad. That's pretty big. Of course, we will typically allocate nowhere even close to that many Quad4s.
• Each Quad4 has a reference to six neighbouring Quad4s; specifically, it knows what Quad4s are to its north, south, west, east, northwest and southeast. A null reference is to be treated as though those cells are all dead. (Why not northeast and southwest? We shall see.)

There are more surprises to come later. Let's write some code. It's pretty straightforward:

sealed class Quad4{ public Quad4(int x, int y) { X = (short)x; Y = (short)y; } // A unique pair of shorts for each 4-quad in a 20-quad. public short X { get; } public short Y { get; } // References to neighbouring Quad4s: public Quad4 N { get; set; } public Quad4 S { get; set; } public Quad4 E { get; set; } public Quad4 W { get; set; } public Quad4 NW { get; set; } public Quad4 SW { get; set; } // Cells private Quad3 evenNW; private Quad3 evenSW; private Quad3 evenNE; private Quad3 evenSE; private Quad3 oddNW; private Quad3 oddSW; private Quad3 oddNE; private Quad3 oddSE; public bool GetEven(int x, int y) { ... } public void SetEven(int x, int y) { ... } public void ClearEven(int x, int y) { ... } public bool GetOdd(int x, int y) { ... } public void SetOdd(int x, int y) { ... } public void ClearOdd(int x, int y) { ... } public string override ToString() { ... }}

Once again those last seven methods are (for now!) just trivial rewrites of the equivalent methods on a Quad2, so I'll omit them here.

Obviously some controlling code representing the entire grid needs to create some number of Quad4s, assign numbers to them, set up the references, and so on. We'll write that code in a later episode; right now I want to continue concentrating on the key problem of stepping to the next tick.

Suppose we are currently on an even generation and we want to step all the Quad4s in the system to the next generation, which will of course be odd. We add this method to Quad4 and have the controlling code call it for every Quad4:

public void StepEven(){ StepEvenNW(); StepEvenSW(); StepEvenNE(); StepEvenSE();}

Pretty straightforward; we step every even Quad3 forward one tick, and presumably that fills in the odd Quad3s. How are we going to do that though?

Time for more diagrams.

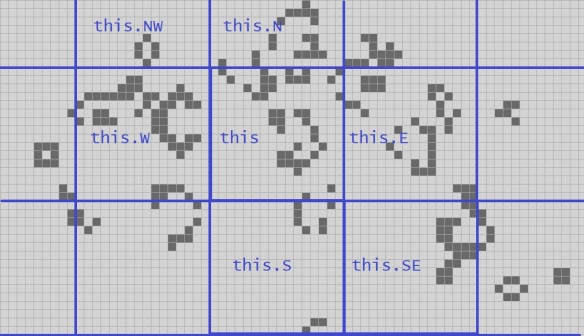
Again I've just randomly chosen a fragment of acorn", this time from generation 416. Let's suppose the 4-quad I've marked as this" is the one we are attempting to step forward one generation. (Click on any image for a higher-res version if one is available.)

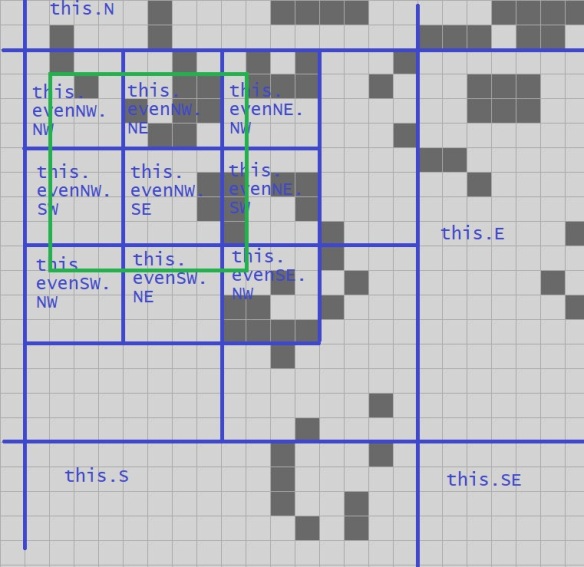
Let's zoom in a bit on this" and give expressions that refer to some interesting Quad2s:

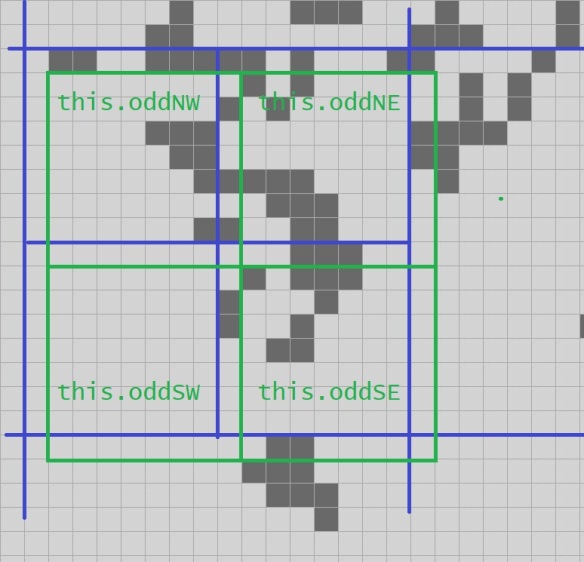
Well would you look at what we have here: nine Quad2s. If we step those forward one step with our handy super-efficient method from last episode, we get the next state of the green Quad3:

The code could not be easier:

private void StepEvenNW(){ oddNW = Step9Quad2ToQuad3( evenNW.NW, evenNW.NE, evenNE.NW, evenNW.SW, evenNW.SE, evenNE.SW, evenSW.NW, evenSW.NE, evenSE.NW);}

I'm going to keep this in its own method though, as I'll be adding more gear to it in an upcoming episode.

That's the easy one, and I don't think I need to labour the point with more diagrams. In order to step forward the other Quad3s we need to be careful about the fact that this.E, this.SE and this.S could be null, but if they are, we just substitute in an all-dead Quad2, which we helpfully made a static field for last time:

private void StepEvenSW(){ oddSW = Step9Quad2ToQuad3( evenSW.NW, evenSW.NE, evenSE.NW, evenSW.SW, evenSW.SE, evenSE.SW, S == null ? AllDead : S.evenNW.NW, S == null ? AllDead : S.evenNW.NE, S == null ? AllDead : S.evenNE.NW);}private void StepEvenNE(){ oddNE = Step9Quad2ToQuad3( evenNE.NW, evenNE.NE, E == null ? AllDead : E.evenNW.NW, evenNE.SW, evenNE.SE, E == null ? AllDead : E.evenNW.SW, evenSE.NW, evenSE.NE, E == null ? AllDead : E.evenSW.NW);}private void StepEvenSE(){ oddSE = Step9Quad2ToQuad3( evenSE.NW, evenSE.NE, E == null ? AllDead : E.evenSW.NW, evenSE.SW, evenSE.SE, E == null ? AllDead : E.evenSW.SW, S == null ? AllDead : S.evenNE.NW, S == null ? AllDead : S.evenNE.NE, SE == null ? AllDead : SE.evenNW.NW);}

And when StepEven returns, we have the next state for the odd generation:

Wait a minute. We have committed the classic programmer blunder of being consistently off by one! We haven't computed the next generation of the even 4-quad; we've computed the next generation of the 4-quad that is the even 4-quad shifted one cell to the southeast.

Well golly.

What are we going to do about this?

Give that some thought and then scroll down.

.

.

.

.

.

.

.

In my youth I was in a group of friends that watched terrible 80s horror movies every week, and we noticed patterns. In particular, in Killer Mutant Critter movies and zombie movies there is often a sheriff, and there are often concerned townsfolk, and the dialog seems to go

Sheriff! Giant mutant toads are attacking the village! What are you going to do about it?!"

Nuthin'."

That's what we're going to do about it. Nuthin'.

This is our final surprise for this episode. A Quad4 represents a 16*16 section of the grid, for two generations, where the odd numbered generation is offset by one cell to the southeast from the even generation. Though this will make life very slightly difficult for the display code, this staggered generations" property turns out to be surprisingly useful; we will see why in an upcoming episode.

Next time on FAIC: The next problem we need to solve is: how are we going to do the odd generation steps? We can't just do the same thing because then we'll be two cells off. Somehow we need to have the odd step get back to the northwest.