Life, part 29

We've built the foundation of the QuickLife algorithm; now let's make it go fast. This is going to be a longer episode than usual because we have a large volume of code to get through to perform a relatively straightforward task, and we won't get through all of it today. Code for this episode is here.

Abrash and Stafford's algorithms both achieved significant wins by maintaining neighbour counts and updating them when something changes. Hensel's QuickLife algorithm does not count neighbours at all! The neighbour counting has been entirely moved to the construction of the lookup table. So there cannot be any savings there.

Stafford's algorithm achieved a significant win by tracking what changes from one tick to the next, but there is a flaw in that plan - or, maybe it would be better to say, there is an opportunity for further optimization.

Suppose we have the simplest possible always-changing grid: a single blinker.

Four cells change on every tick: two are born and two die. Stafford's algorithm works on triples; for every tick we need to consider on the order of a dozen triples that might be changing next.

Now consider the gear we have built so far for QuickLife: we have the state of one even and one odd generation saved. Who cares whether there is a difference between the even generation and the odd generation? In the example above every even generation is the same as every other, and every odd generation is the same as every other.

Period-two oscillators are extremely common in Life, but from QuickLife's perspective, given that it saves two generations in every Quad4, period-two oscillators could be treated as still Lifes! And remember that of course that still Lifes are also period-two oscillators; they just have the same state in both cycles.

In short: If we know that for some region of a quad4 the next even generation is the same as the previous even generation, then we can skip all computations on that region, and similarly for the odd generations. That works right up until the point where some active" cells in a neighbouring region get close enough to the stable region to destabilize it.

It seems like there is a powerful optimization available here; how are we going to achieve it?

Let's start by crisping up the state that we are tracking. We will be considering rectangular regions" of a Quad3, and classifying them into three buckets:

• Active - a cell changed value from the previous generation to the next generation. That is, if we are currently in generation 3, stepping to even generation 4, then we check to see whether the region in question is the same as it was in generation 2.
• Stable - a region which is not active; every cell in the region is going to be the same in the next generation as it was in the previous generation.
• Dead - a region which is stable, and moreover, every cell in the region is dead

Notice that there is a subtlety here: a region can be entirely dead cells but is still considered active if it just recently became all dead. A region does not become classified as dead until it is both stable and all dead cells.

What regions do we care about? For odd generation Quad3s we will classify the following regions as dead, stable or active:

• The entire Quad3

That is, did anything at all in these 64 cells change? and if not, are any of them alive?

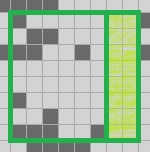
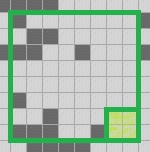
• The 2*8 eastern edge:

• The 8*2 southern edge:

• And finally, the 2*2 southeastern corner:

For the even generation Quad3s, we will track the same stuff, except different. For evens, we track the state of:

• The entire Quad3
• The 2*8 western edge
• The 8*2 northern edge
• The 2*2 northwest corner

That sounds like a lot of information to deal with: we've got three possible states for each of four regions of each of eight Quad3s in a Quad4. Of course, we're going to deal with it by twiddling bits, and of course I am going to encapsulate every bit operation into a helper method with a sensible name.

Our bit format will be as follows.

• Each of the eight Quad3s in a Quad4 will have eight bits of state data.
• Those 64 bits will be stored in two uints, one for the evens, one for the odds, and they will be fields of Quad4.
• Bits 0-7 will be for the SE Quad3, bits 8-15 the NE, 16-23 the SW and 24-31 the NW

Pretty straightforward so far. What does each of the eight bits in the byte associated with a Quad3 mean? We consider the bits in pairs.

• bits 0 and 4 give the state of the SE (odd) or NW (even) corner
• bits 1 and 5 give the state of the south/north edge
• bits 2 and 6 give the state of the east/west edge
• bits 3 and 7 give the state of the Quad3 as a whole
• If both bits are off, then the region is active
• If both bits are on, then the region is dead
• If the lower bit is on and the higher is off, then the region is stable
• The higher bit is never turned on if the lower bit is off.

This scheme has some nice properties:

• If you want to check for not active" you just have to look at the low bit
• If you want to check for dead" you just have to look at the high bit
• If you want to set a region to stable" and it is already marked dead", that's OK, it stays dead
• And so on

But because I am only going to access these bits via helper functions, it really doesn't matter what the format is so long as we get all the transitions correct.

I'm going to make a helper struct for the setters, solely to make the code easier to read. (Why just the setters? We will see in the next episode. Foreshadowing!) We will never store one of these, so there is no reason to make it wrap a byte instead of a uint; no reason to make the runtime truncate it on each operation.

struct Quad3State{ readonly private uint b; public Quad3State(int b) => this.b = (uint)b; public Quad3State(uint b) => this.b = b; public Quad3State SetAllRegionsActive() => new Quad3State(0x00); public Quad3State SetVerticalEdgeAndQuadActive() => new Quad3State(b & 0x33); public Quad3State SetHorizontalEdgeAndQuadActive() => new Quad3State(b & 0x55); public Quad3State SetQuad3Active() => new Quad3State(b & 0x77); public Quad3State SetAllRegionsStable() => new Quad3State(b | 0xf); public Quad3State SetVerticalEdgeStable() => new Quad3State(b | 0x04); public Quad3State SetHorizontalEdgeStable() => new Quad3State(b | 0x02); public Quad3State SetCornerStable() => new Quad3State(b | 0x01); public Quad3State SetAllRegionsDead() => new Quad3State(0xff); public Quad3State SetVerticalEdgeDead() => new Quad3State(b | 0x44); public Quad3State SetHorizontalEdgeDead() => new Quad3State(b | 0x22); public Quad3State SetCornerDead() => new Quad3State(b | 0x11); public static explicit operator uint(Quad3State s) => s.b;}

A few things to notice here:

• Calling a set stable" helper keeps the dead" bit set if it is already set, which is what we want. If we've deduced that a region is stable and we already know it is dead, that's fine.
• When we set an edge to active we set the whole Quad3 to active also, since plainly if there is activity in the edge, there is activity in the Quad3.
• Contradicting the previous point, when we set an edge to stable or dead, we do not set the corner contained in that edge region to stable or dead, even though obviously it is; we cannot have the entire edge be stable and its corner be unstable. It just so happens that in the original implementation, every code path on which the edge is set to stable, the corner has already been set to stable, and I will maintain this property in my port. It wouldn't hurt to fix that here, but I wanted to match the behaviour of the original code as much as possible.
• There is no set corner active" because if you're setting the corner active, you're setting all the regions active.

All right, we have our helper to set state for a Quad3. We need eight state bytes, one for each of the eight Quad3s in a Quad4. We declare our state words as fields in Quad4:

private uint evenstate;private uint oddstate;

And make eight helpers to shift the state bits in and out:

private Quad3State EvenSEState{ get => new Quad3State(evenstate & 0x000000ff); set => evenstate = (evenstate & 0xffffff00) | (uint)value;}...

Suppose we're on an odd generation and we've just computed the next (even) generation for the NW Quad3. We have the previous even generation in hand; how are we going to know which setters to call? We need to figure out two things:

• Given an old Quad3 and a new one, which regions of the new one are different?
• Of the regions that are not different, which of them are all dead?

I mentioned in a previous episode that I was one day going to add more code to the step a Quad3" methods in Quad4, and that day has come. Remember that the original code was:

private void StepOddNW(){ evenNW = Step9Quad2ToQuad3Odd( ... );}

The new method is:

private void StepOddNW(){ Quad3 newEvenNW = Step9Quad2ToQuad3Odd( ... ); EvenNWState = evenNW.UpdateEvenQuad3State(newEvenNW, EvenNWState); evenNW = newEvenNW;}

That is: compute the next even generation, update the state bits by comparing the previous even generation to the next even generation, and then set the new state bits and new even NW Quad3.

How does the UpdateEvenQuad3State work? Plainly we have to compare the previous generation's Quad3 to the newly computed Quad3, and in particular we will need to know if any of its regions are dead.

Let's start with solving the even simpler problem: which regions are composed of all dead cells? I'm going to add these helper functions to Quad3:

bool AllDead => (NW | NE | SW | SE).Dead;bool NorthwestCornerDead => NW.NW.Dead;bool SoutheastCornerDead => SE.SE.Dead;bool NorthEdgeDead => (NW | NE).NorthEdge.Dead;bool WestEdgeDead => (SW | NW).WestEdge.Dead;bool SouthEdgeDead => (SW | SE).SouthEdge.Dead;bool EastEdgeDead => (NE | SE).EastEdge.Dead;

That is, OR together the relevant portions of each component Quad2, mask out the irrelevant portions, and check whatever is left for deadness.

Notice that I've made these private; we'll put all the code that needs these in Quad3. (I told you these helper types were not going to stay simple!)

How will we compute what parts are stable? If we have a previous Quad3 in hand and a new Quad3, we need to know what regions are unchanged. The XOR operation gives us that on bits; XOR is one if the bits are different and zero if they are the same. I'll add an XOR operation to Quad2, just like we have an OR operation already:

public static Quad2 operator ^(Quad2 x, Quad2 y) => new Quad2((ushort)(x.cells ^ y.cells));

Remember that my goal for this series is to make the code as clear as possible by making it read like business domain" code rather than mechanism domain" code. I need to know what regions of a Quad3 have changed, so I'm going to do that by making a new struct called change report" that gives a pleasant, readable interface overtop of the bit-twidding mechanisms. In Quad3:

private Quad3ChangeReport Compare(Quad3 q) => new Quad3ChangeReport(this, q);

The implementation is basically just a rename of the operations we just added to Quad3!

private struct Quad3ChangeReport{ public Quad3ChangeReport(Quad3 x, Quad3 y) { q3 = new Quad3(x.NW ^ y.NW, x.NE ^ y.NE, x.SW ^ y.SW, x.SE ^ y.SE); } private readonly Quad3 q3; public bool NoChange => q3.AllDead; public bool NorthwestCornerNoChange => q3.NorthwestCornerDead; public bool SoutheastCornerNoChange => q3.SoutheastCornerDead; public bool NorthEdgeNoChange => q3.NorthEdgeDead; public bool WestEdgeNoChange => q3.WestEdgeDead; public bool SouthEdgeNoChange => q3.SouthEdgeDead; public bool EastEdgeNoChange => q3.EastEdgeDead;}

Adding a few extra lines of code in order to make the call sites readable is very worthwhile in my opinion. Remember, the jitter is pretty smart and will inline these operations, and if it doesn't, well, it is easier to make a readable program more performant than an unreadable one.

Note also that this struct is nested inside Quad3, so that it can use the private helper methods I just added. I don't often program with nested types, but this is an ideal use case; it is an implementation detail of a method of the outer type.

We've digressed slightly from the question at hand: how do we update state bits given old state bits, an old Quad3 and a new Quad3?

I know the following method looks a little bit hard to read, but imagine how it looks with every one of those bit-twiddling operations written out as a bit operation with a hexadecimal mask! Believe me, it is more understandable when you can read the business logic in English:

public Quad3State UpdateEvenQuad3State(Quad3 newQ3, Quad3State s){ Quad3ChangeReport changes = newQ3.Compare(this); if (changes.NorthwestCornerNoChange) { if (newQ3.NorthwestCornerDead) s = s.SetCornerDead(); else s = s.SetCornerStable(); if (changes.NorthEdgeNoChange) { if (newQ3.NorthEdgeDead) s = s.SetHorizontalEdgeDead(); else s = s.SetHorizontalEdgeStable(); } else { s = s.SetHorizontalEdgeAndQuadActive(); } if (changes.WestEdgeNoChange) { if (newQ3.WestEdgeDead) s = s.SetVerticalEdgeDead(); else s = s.SetVerticalEdgeStable(); if (changes.NoChange) { if (newQ3.AllDead) s = s.SetAllRegionsDead(); else s = s.SetAllRegionsStable(); } else { s = s.SetQuad3Active(); } } else { s = s.SetVerticalEdgeAndQuadActive(); } } else { s = s.SetAllRegionsActive(); } return s;}

If you trace all the logic through you'll see that with only a handful of bit operations we manage to correctly update the eight state bits for the even-cycle Quad3.

We then cut-n-paste this code to do the same thing to the odd cycle, just looking at the opposite edges and corners; obviously I'll omit that.

Once again we've managed to write a whole lot of bit-twiddling code; we now know at the end of every tick whether each of thirty-two regions of a Quad4 had any change from how they were two generations previous.

How are we going to use this information to save time?

Next time on FAIC: We'll write getters to read out the state we've just written, and draw a bunch more diagrams.