Sum of divisor powers
The function k takes an integer n and returns the sum of the kth powers of divisors of n. For example, the divisors of 14 are 1, 2, 4, 7, and 14. If we set k = 3 we get
3(n) = 1^3 + 2^3 + 4^3 + 7^3 + 14^3 = 3096.
A couple special cases may use different notation.
- 0(n) is the number of divisors n and is usually denoted d(n), as in the previous post.
- 1(n) is the sum of the divisors of n and the function is usually written (n) with no subscript.
In Python you can compute k(n) using divisor_sigma from SymPy. You can get a list of the divisors of n using the function divisors, so the bit of code below illustrates that divisor_sigma computes what it's supposed to compute.
n, k = 365, 4 a = divisor_sigma(n, k) b = sum(d**k for d in divisors(n)) assert(a == b)
The Wikipedia article on k gives graphs for k = 1, 2, and 3 and these graphs imply that k gets smoother as k increases. Here is a similar graph to those in the article.
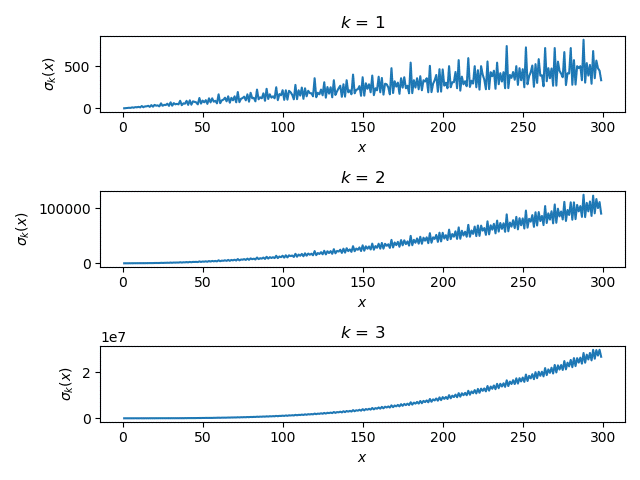
The plots definitely get smoother as k increases, but the plots are not on the same vertical scale. In order to make the plots more comparable, let's look at the kth root of k(n). This amounts to taking the Lebesgue k norm of the divisors of n.
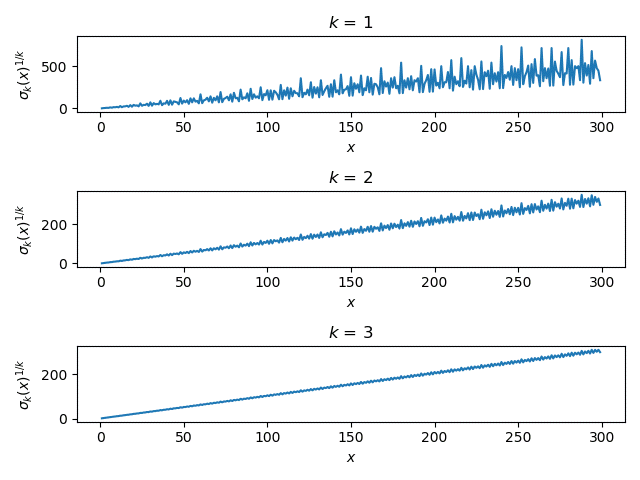
Now that the curves are on a more similar scale, let's plot them all on a single plot rather than in three subplots.
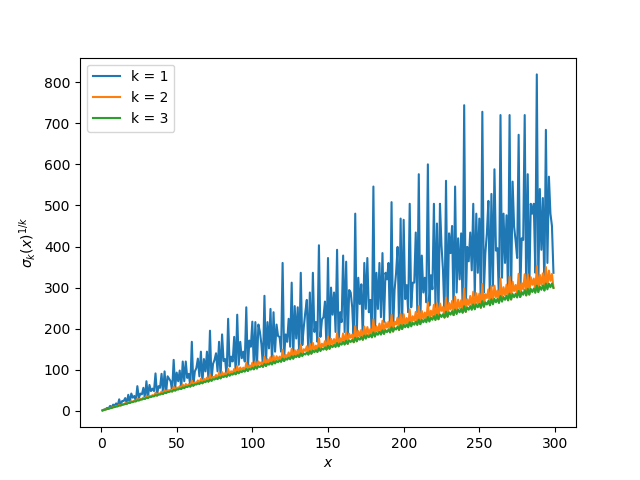
If we leave out k = 1 and add k = 4, we get a similar plot.
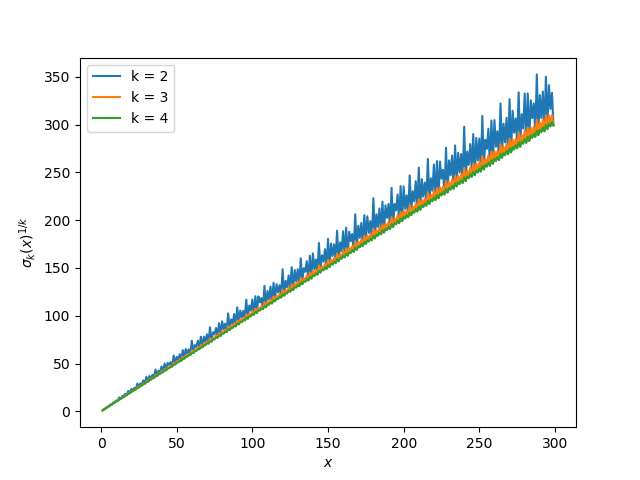
The plot for k = 2 that looked smooth compared to k = 1 now looks rough compared to k = 3 and 4.
The post Sum of divisor powers first appeared on John D. Cook.