Superfactorial

The factorial of a positive integer n is the product of the numbers from 1 up to and including n:

n! = 1 * 2 * 3 * ... * n.

The superfactorial of n is the product of the factorials of the numbers from 1 up to and including n:

S(n) = 1! * 2! * 3! * ... * n!.

For example,

S(5) = 1! 2! 3! 4! 5! = 1 * 2 * 6 * 24 * 120 = 34560.

Here are three examples of where superfactorial pops up.

Vandermonde determinant

If V is the n by n matrix whose ij entry is i^j-1 then its determinant is S(n-1). For instance,

V is an example of a Vandermonde matrix.

Permutation tensor

One way to define the permutation symbol uses superfactorial:

Barnes G-function

The Barnes G-function extends superfactorial to the complex plane analogously to how the gamma function extends factorial. For positive integers n,

Here's plot of G(x)

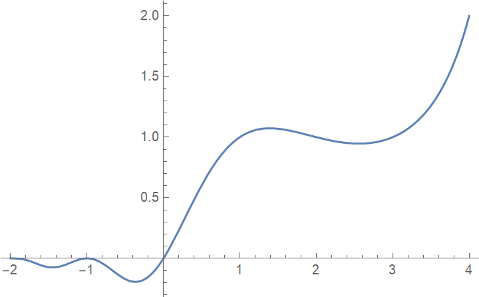
produced by

 Plot[BarnesG[x], {x, -2, 4}]

in Mathematica.

More posts related to factorial

• Any number can start a factorial
• Alternating sums of factorials
• Defining zero factorial
• Variations on factorial
• How to compute log factorial

The post Superfactorial first appeared on John D. Cook.