Ripples and hyperbolas
I ran across a paper [1] this morning on the differential equation
y = sin(xy).
The authors recommend having students explore numerical solutions to this equation and discover theorems about its solutions.
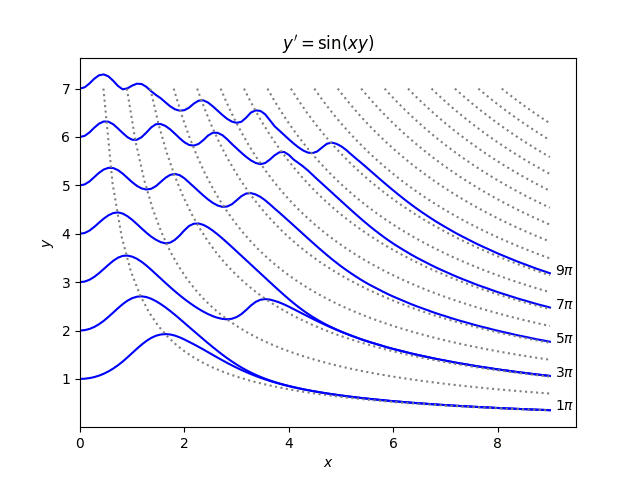
Their paper gives numerous theorems relating solutions and the hyperbolas xy = a: how many times a solution crosses a hyperbola, at what angle, under what conditions a solution can be tangent to a hyperbola, etc.
The plot above is based on a plot in the original paper, but easier to read. It wasn't so easy to make nice plots 40 years ago. In the original plot the solutions and the asymptotes were plotted with the same thickness and color, making them hard to tell apart.
More differential equation posts[1] Wendell Mills, Boris Weisfeiler and Allan M. Krall. Discovering Theorems with a Computer: The Case of y = sin(xy). The American Mathematical Monthly, Nov., 1979, Vol. 86, No. 9 (Nov., 1979), pp. 733-739
The post Ripples and hyperbolas first appeared on John D. Cook.