Drawing commutative diagrams with Quiver
I recently discovered quiver, a tool for drawing commutative diagrams. It looks like a nice tool for drawing diagrams more generally, but it's designed particularly to include the features you need when drawing the kinds of diagrams that are ubiquitous in category theory.
You can draw diagrams using the online app and export the result to LaTeX (tikz).
Here are some examples.
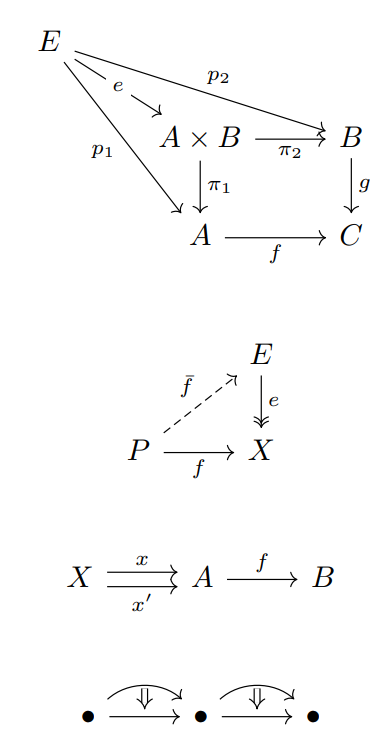
The app is mostly easy to figure out. The object and arrow labels are specified using LaTeX.
Quiver lets you position labels on either side of an arrow, or even inside the arrow as in the e in the first diagram above.
You can change the arrow and arrowhead styles, as in the second example.
It took me a little while to figure out how to have two arrows with the same destination and source, as in the third example. You use the offset" setting to move arrows up or down do that they're not on top of each other. And by default, the software helpfully assumes that if you want to move one arrow up a bit from center, you probably want to move the other one down from center by the same amount.
You can use the curve" setting to draw arrows as in the final example. You can also draw arrows between arrows, as is common when working with 2-categories.
More category theory posts- How category theory is applied
- Categorical products
- Why is an empty sum 0 and an empty product 1?
- Applied category theory
The post Drawing commutative diagrams with Quiver first appeared on John D. Cook.