A generalization of sine and cosine
David Shelupsky [1] suggested a generalization of sine and cosine based on solutions to the system of differential equations
with initial conditions s(0) = 0 and s(0) = 1.
If s = 2, then (t) = sin(t) and (t) = cos(t). The differential equations above reduce to the familiar fact that the derivative of sine is cosine, and the derivative of cosine is negative sine.
For larger even values of s, the functions s and s look like sine and cosine respectively, though flatter at their maxima and minima. Numerical experiments suggest that the solutions are periodic and the period increases with s. [2]
Here's a plot for s = 4.
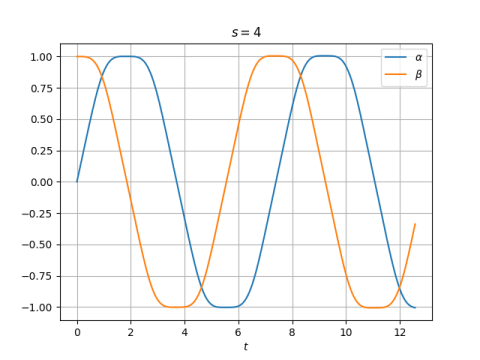
The first zero of (t) is at 3.7066, greater than . In the plot t ranges from 0 to 4, but the second period isn't finished.
If we look at the phase plot, i.e ((t), (t)), we get a shape that I've blogged about before: a squircle!
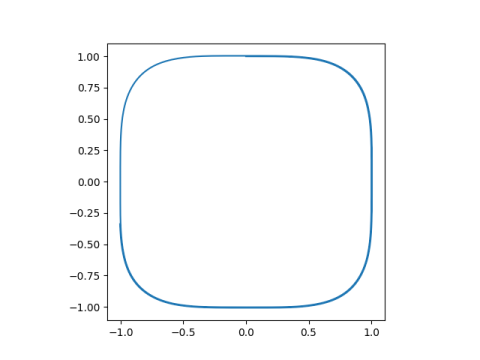
This is because, as Shelupsky proved,
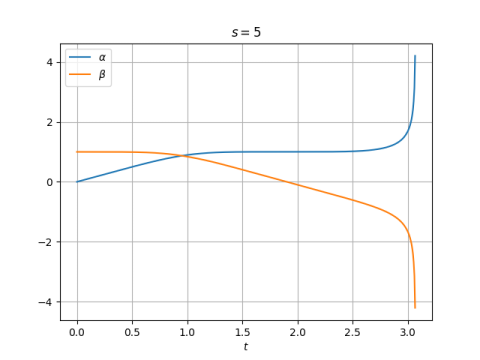
The comments above mostly concern the case of even s. When s is odd, functions s and s don't seem much like sine or cosine. Here are plots for s = 3
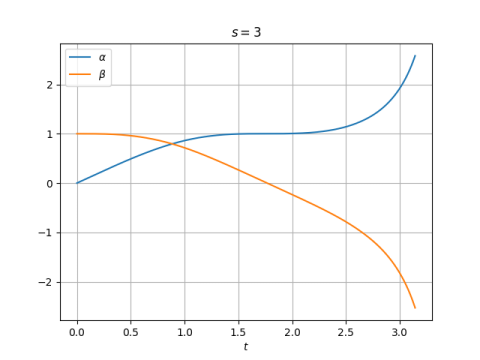
and s = 5.
[1] David Shelupsky. A Generalization of the Trigonometric Functions. The American Mathematical Monthly, Dec. 1959, pp. 879-884
[2] After doing my numerical experiments I looked back more carefully at [1] and saw that the author proves that the solutions for even values of s are periodic, and that the periods increase with s, converging to 4 as s goes to infinity.
The post A generalization of sine and cosine first appeared on John D. Cook.