Large matrices rarely have saddlepoints
A matrix is said to have a saddlepoint if an element is the smallest element in its row and the largest element in its column. For example, 0.546 is a saddlepoint in the matrix below because it is the smallest element in the third row and the largest element in the first column.
In [1], Goldman considers the probability of an m by n matrix having a saddlepoint if its elements are chosen independently at random from the same continuous distribution. He reports this probability as
but it may be easier to interpret as
When m and n are large, the binomial coefficient in the denominator is very large.
For square matrices, m and n are equal, and the probability above is 2n/(n + 1) divided by the nth Catalan number Cn.
A couple years ago I wrote about bounds on the middle binomial coefficient
by E. T. H. Wang. These bounds let us conclude that P(n, n), the probability of an n by n matrix having a saddlepoint, is bounded as follows.
Here's a plot of P(n, n) and its bounds.
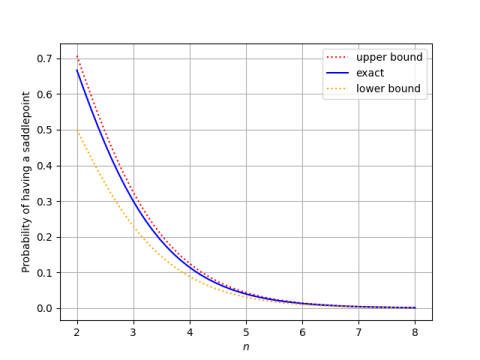
This shows that the probability goes to zero exponentially as n increases, being impossible to visually distinguish from 0 in the plot above when n = 8.
The upper bound on P(n, n) based on Wang's inequalities is tighter than the corresponding lower bound. This is because Wang's lower bound on the middle binomial coefficient is tighter (see plot here) and we've taken reciprocals.
SimulationThe theory above says that if we generate 4 by 3 matrices with independent normal random values, each matrix with have a saddle point with probability 1/5. The following code generates 10,000 random 4 by 3 matrices and counts what proportion have a saddle point.
import numpy as np from scipy.stats import norm def has_saddlepoint(M): m, n = M.shape row_min_index = [np.argmin(M[i,:]) for i in range(m)] col_max_index = [np.argmax(M[:,j]) for j in range(n)] for i in range(m): if col_max_index[row_min_index[i]] == i: return True return False m, n = 4, 3 N = 10000 saddlepoints = 0 for _ in range(N): M = norm.rvs(size=(m,n)) if has_saddlepoint(M): saddlepoints += 1 print(saddlepoints / N)
When I ran this, I got 0.1997, very close to the expected value.
More on random matrices[1] A. J. Goldman. The Probability of a Saddlepoint. The American Mathematical Monthly, Vol. 64, No. 10, pp. 729-730
The post Large matrices rarely have saddlepoints first appeared on John D. Cook.