Random polynomials revisited
A few days ago I wrote about the expected number of roots in a random polynomial where each coefficient is drawn from a standard normal, i.e. a Gaussian distribution with mean 0 and variance 1.
Another class of random polynomials, one that comes up in applications to physics, draws each coefficient from a different distribution. Specifically, the nth coefficient in an Nth degree polynomial is drawn from a normal distribution with mean zero and variance N choose n. As before, our reference is [1].
It turns out that for these random polynomials, the expected number of real zeros is N. This is not an asymptotic approximation.
For an example, I created a random 44th degree polynomial.
from scipy.stats import norm from scipy.special import binom N = 44 coeff = [norm.rvs(scale=binom(N,n)**0.5) for n in range(N+1)]
I plotted the (tanh of) this polynomial as described here.
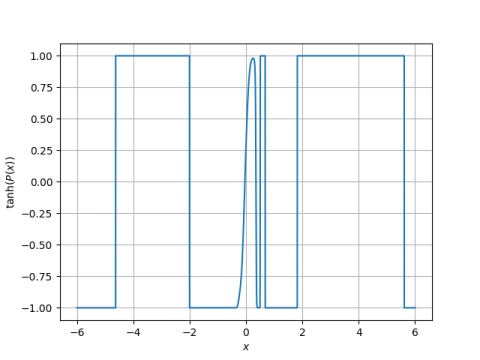
This polynomial clearly has 8 real roots. The expected number of roots for a 44th degree random polynomial of this type is 44 = 6.63.
[1] Alan Edelman and Eric Kostlan. How many zeros of a random polynomial are real? Bulletin of the AMS. Volume 32, Number 1, January 1995
The post Random polynomials revisited first appeared on John D. Cook.