Pythagorean chaos

If a and b are two distinct positive integers, then

|a^2-b^2|, 2ab, a^2+b^2

is a Pythagorean triple. The result still gives the sides of a right triangle if the starting points aren't integers

In [1], Nick Lord looks at what happens if you iterate this procedure, using the output of one step as the input to the next step, and look at the smaller angle of the right triangle that results.

The numbers grow exponentially, so it helps to divide a and b by c on each iteration. This prevents the series from overflowing but doesn't change the angles.

Here's a little Python code to explore the sequence of angles.

 import numpy as np  = np.empty(50000, dtype=float) a, b = np.random.random(2) for i in range(1, N-1): c = a**2 + b**2 a, b = abs(a**2 - b**2)/c, 2*a*b/c [i] = min( np.arctan(a/b), np.arctan(b/a) )

Here's what we get if we plot the first 100 angles.

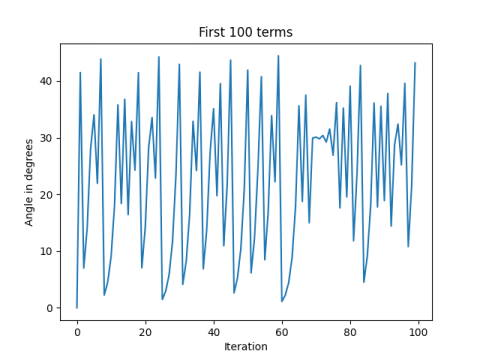
As Lord points out in [1], the series is chaotic.

Here's a histogram of the angles.

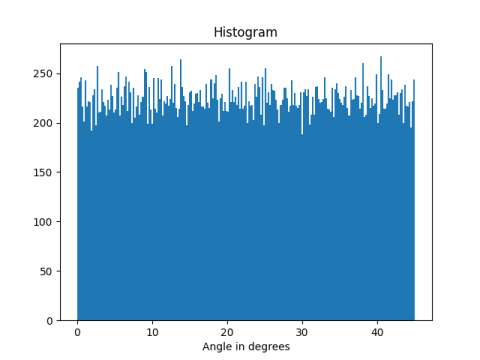
[1] Nick Lord. Maths bite: Pythagoras causes chaos! The Mathematical Gazette, Vol. 92, No. 524 (July 2008), pp. 290-292.

The post Pythagorean chaos first appeared on John D. Cook.