Simple trig function approximations

Anthony Robin gives three simple approximations for trig functions in degrees in [1].

The following plots show that these approximations are pretty good. It's hard to distinguish the approximate and exact curves.

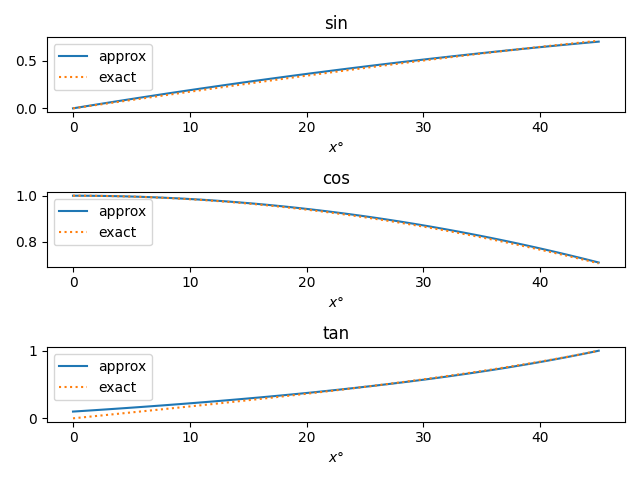
The accuracy of the approximations is easier to see when we subtract off the exact values.

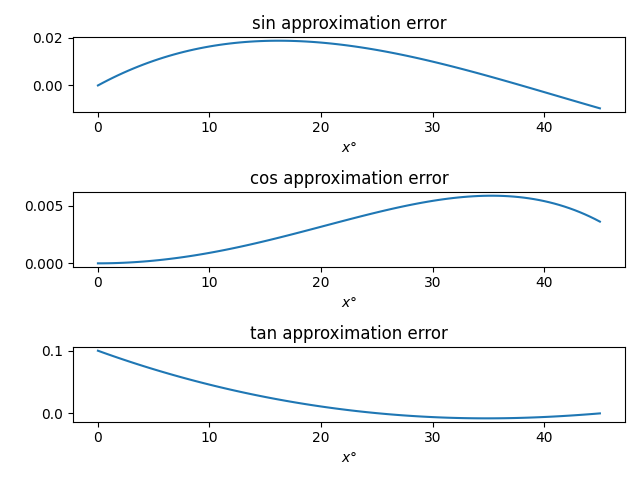
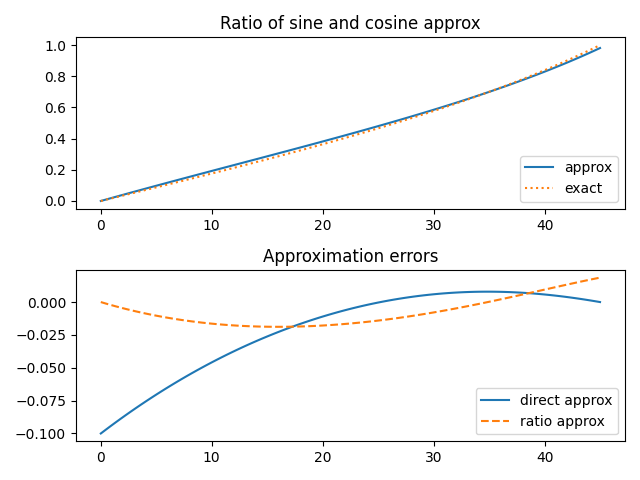
The only problem is that the tangent approximation is poor for small angles [2]. The ratio of the sine and cosine approximations makes a much better approximation, but it this requires more work to evaluate. You could use the ratio for small angles, say less than 20, and switch over to the tangent approximation for larger angles.

Here's the Python code that was used to create the plots in this post. It uses one trick you may find interesting, using the eval function to between the names of functions and the functions themselves.

from numpy import sin, cos, tan, linspace, deg2radimport matplotlib.pyplot as pltsin_approx = lambda x: 0.01*x*(2-0.01*x)cos_approx = lambda x: 1 - x*x/7000.0tan_approx = lambda x: (10.0 + x)/(100.0 - x)trig_functions = ["sin", "cos", "tan"];x = linspace(0, 45, 100)fig, ax = plt.subplots(3,1)for n, trig in enumerate(trig_functions): ax[n].plot(x, eval(trig + "_approx(x)")) ax[n].plot(x, eval(trig + "(deg2rad(x))"), ":") ax[n].legend(["approx", "exact"]) ax[n].set_title(trig) ax[n].set_xlabel(r"$x\degree$")plt.tight_layout()plt.savefig("trig_approx_plot.png")fig, ax = plt.subplots(3,1)for n, trig in enumerate(trig_functions): y = eval(trig + "_approx(x)") z = eval(trig + "(deg2rad(x))") ax[n].plot(x, y-z) ax[n].set_title(trig + " approximation error") ax[n].set_xlabel(r"$x\degree$")plt.tight_layout()plt.savefig("trig_approx_error.png")tan_approx2 = lambda x: sin_approx(x)/cos_approx(x)fig, ax = plt.subplots(2, 1)y = tan(deg2rad(x))ax[0].plot(x, tan_approx2(x))ax[0].plot(x, y, ":")ax[0].legend(["approx", "exact"], loc="lower right")ax[0].set_title("Ratio of sine and cosine approx")ax[1].plot(x, y - tan_approx(x), "-")ax[1].plot(x, y - tan_approx2(x), "--")ax[1].legend(["direct approx", "ratio approx"])ax[1].set_title("Approximation errors")plt.tight_layout()plt.savefig("tan_approx.png")

Related posts

• Calculating normal probabilities with a simple calculator
• Trig functions across programming languages

[1] Anthony C. Robin. Simple Trigonometric Approximations. The Mathematical Gazette, Vol. 79, No. 485 (Jul., 1995), pp. 385-387

[2] When I first saw this I thought No big deal. You can just use tan for small angles, or tan + ^3/3 if you need more accuracy." But these statements don't apply here because we're working in degrees, not radians.

tan is not approximately for small angles but rather approximately / 180. If you're working without a calculator you don't want to multiply by if you don't have to, and a calculator that doesn't have keys for trig functions may not have a key for .

The post Simple trig function approximations first appeared on John D. Cook.