Hypotenuse approximation

Ashley Kanter left a comment on Tuesday's post Within one percent with an approximation I'd never seen.

One that I find handy is the hypotenuse of a right-triangle with other sides a and b (where a<b) can be approximated to within 1% by 5(a+b)/7 when 1.04 b/a 1.50.

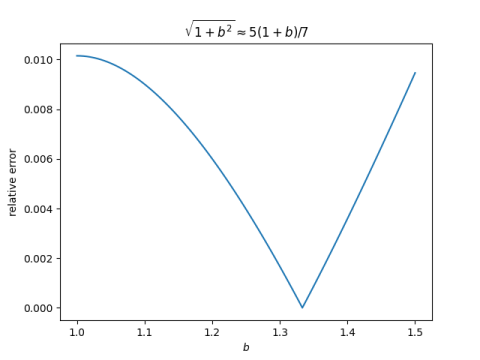
That sounds crazy, but it's right. Since we're talking about relative error, not absolute error, we can assume without loss of generality that a = 1. Here's a plot of the relative error in the approximation.

Here's the Python code that produced the plot.

 from numpy import linspace import matplotlib.pyplot as plt exact = lambda b: (b**2 + 1)**0.5 approx = lambda b: 5*(1+b)/7 rel_error = lambda b: abs((exact(b) - approx(b))/exact(b)) x = linspace(1, 1.5, 100) plt.plot(x, rel_error(x)) plt.xlabel("$b$") plt.ylabel("relative error") plt.title(r"$\sqrt{1+b^2} \approx 5(1+b)/7$") plt.savefig("hyp_approx.png")

You can solve a quadratic equation to find that the error is zero at b = 4/3. In fact, this gives a clue to where the approximation came from: it is exact for a (3, 4, 5) triangle.

Let's see where the relative error equals 0.01.

 from scipy.optimize import bisect left = bisect(lambda b: rel_error(b) - 0.01, 0.0, 1.3) right = bisect(lambda b: rel_error(b) - 0.01, 1.4, 1.6) print(left, right)

This shows that the approximation is within 1% over the interval [1.0354, 1.5087], or to use rounder numbers, [1.04, 1.50] as advertised. The error is only 1.02% if you take the interval to be [1, 1.50]. So if you take approximately equal" to mean within 1.02%" then we can restate the rule above as

If one leg of a right triangle is no more than 50% bigger than the other, then the hypotenuse is approximately 5(a+b)/7.

On a similar note, see this post about the case where b is much larger than a. If you want to measure across a room, for example, and you can't quite measure to the point you'd like, it makes surprisingly little difference.

The post Hypotenuse approximation first appeared on John D. Cook.