Tower of powers and convergence
This post will look at the tower of powers"
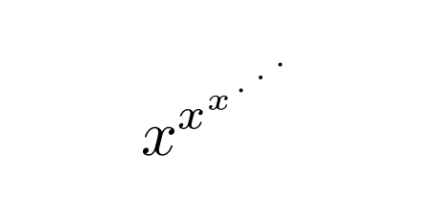
and ask what it means, when it converges, and how to compute it. Along the way I'll tie in two recent posts, including one that should come as a surprise.
First of all, the expression is right-associative. That is, it is the limit of
x^(x^(x^...))
and not the limit of
((x^x)^x)^...)
This means we evaluate our tower from the top down, which is a little strange to think about. But if we interpreted our tower as left-associative, building the tower from the bottom up, the sequence would be much less interesting: the limit would be 1 for 0 < x 1, and infinity for x > 1.
A few weeks ago I wrote about the special case of x equal to the imaginary unit. I looked at the sequence
and the pattern the it makes in the complex plane.
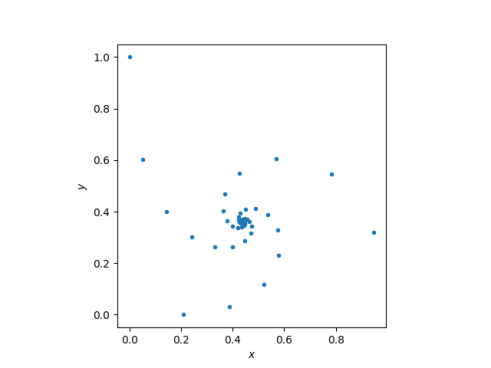
We can see that the iterates converge to somewhere around 0.4 + 0.4i.
This post will replace i with a real number x. Leonard Euler discovered a long time ago that the tower of power" converges for x between e-e and e1/e. See[1].
Furthermore, for those xs where the sequence converges, it converges to an expression involving the Lambert W function which I wrote about in my previous post.
The power tower can be written in Donald Knuth's up arrow notation as the limit of
as n goes to infinity. The equation relating this limit to Lambert's W function is
Let's try this out numerically. Euler tells us the limit exists for x in the interval [e-e , e1/e] which is roughly [0.07, 1.44].
We'll do this at the Python REPL. First we import functions to compute log and W.
>>> from math import log >>> from scipy.special import lambertw as w
Now if we have correctly found our limit y, then xy should equal y. The following shows that this is the case.
>>> x = 0.07 >>> y = -w(-log(x))/log(x) >>> y 0.37192832251839264 >>> x**y 0.37192832251839264 >>> x = 1.44 >>> y = -w(-log(x))/log(x) >>> y 2.3938117482029475 >>> x**y 2.393811748202947
By the way, we've said which real values of x cause the series to converge. But my first post on iterated powers looked at x = i. For which complex values does the series converge? I suspect the domain is a complicated fractal, but I don't know that for sure.
Related posts[1] Brian Hayes. Why W? American Scientist. Vol 93, pp 104-109.
The post Tower of powers and convergence first appeared on John D. Cook.