Generalizing Shannon entropy with q-logs

The most common way to quantify entropy is Shannon entropy. That's what people usually mean when they say entropy" without further qualifications. A while back I wrote about Renyi entropy as a generalization of Shannon entropy. This time I'll explore a different generalization called q-log entropy, a.k.a. Tsallis entropy.

The definition of Shannon entropy includes the logarithms of probabilities. If we replace these logarithms with a generalization of logarithms, we have a generalization of Shannon entropy.

q-logarithms

The generalization of logarithm we want to look at for this post is the q-logarithm. The natural logarithm is given by

and we can generalize this to the q-logarithm by defining

And so ln₁ = ln.

q-logarithm entropy

We can define q-log entropy (a.k.a. Tsallis entropy) by replacing natural log with q-log. However we run into a minor issue.

Shannon entropy (in nats, see [1]) can be defined as either

or

These are equivalent because

However

unless q = 1.

On the other hand, it's easy to show that

And so we could use either ln_q(1/p) or -ln_q(p) in our definition of q-log entropy.

The two definitions are not equivalent unless q = 1, but they are related by

Example

To see q-log entropy in action, we'll plot the entropy of the English alphabet as q varies.

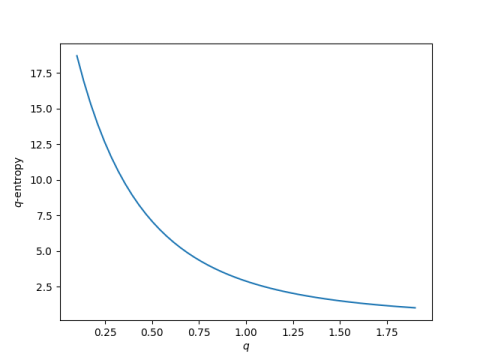
This plot was made using English letter frequencies from here and the following Python code.

 def lnq(x, q): if q == 1: return np.log(x) t = 1 - q return (x**t - 1) / t def shannon_entropy(ps, base=2): s = sum(p*np.log(1/p) for p in ps) return s/np.log(base) def qlog_entropy(ps, q): return sum(p*lnq(1/p, q) for p in ps)

The Shannon entropy of the English alphabet is 2.8866 nats [2]. The q-log entropy is greater than that for q less than 1, and smaller than that for q greater than 1.

Related posts

• Solving for probability given entropy
• How fast were ancient languages spoken?
• Bits of information in a zip code

[1] Shannon entropy is usually defined in terms of logarithms base 2, i.e. entropy is usually measured in bits. If we change the base of the logarithm, we only multiply the result by a constant. So we can define Shannon entropy using natural logarithms, resulting in entropy measured in nats." More on bits, dits, and nats here.

[2] Or 4.1645 bits. See [1] above for the difference between bits and nats.

The post Generalizing Shannon entropy with q-logs first appeared on John D. Cook.