Simple derivation of exponential approximation
I was watching one of Brian Douglas' videos on control theory (Discrete Control #5) and ran into a simple derivation of an approximation I presented earlier.
Back in April I wrote several post on simple approximations for log, exp, etc. In this post I gave an approximation for the exponential function:
The control theory video arrives at the same approximation as follows.
As I believe I've suggested before here, in a derivation like the one above, where you have mostly equalities and one or two approximations, pay special attention to the approximation steps. The approximation step above uses a first order Taylor approximation in the numerator and denominator.
The plot below shows that the approximation above (the bilinear approximation) is more accurate than doing a single Taylor approximation, approximating exp(x) by 1 + x (linear approximation).
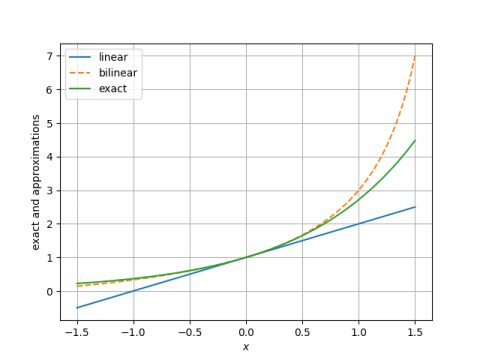
Here's a plot focusing on the error in the bilinear and linear approximations.
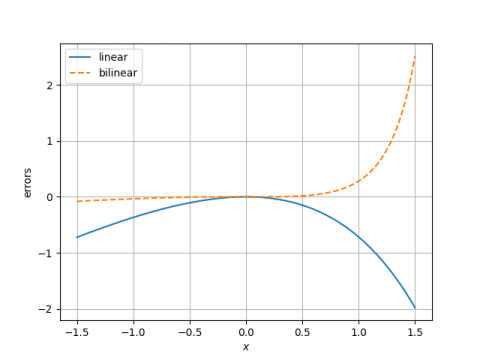
The bilinear approximation is hard to tell from 0 in the plot above for x up to 0.5.
The derivation above is simple, but why is the result so good? An explanation in terms of Pade approximation is given here.
The post Simple derivation of exponential approximation first appeared on John D. Cook.