50 sigma events for t distributions

I had a recent discussion with someone concerning a 50 sigma event, and that conversation prompted this post.

When people count sigmas" they usually have normal distributions in mind. And six-sigma events so rare for normal random variables that it's more likely the phenomena under consideration doesn't have a normal distribution. As I explain here,

If you see a six-sigma event, that's evidence that it wasn't really a six-sigma event.

If six-sigma events are hard to believe, 50-sigma events are absurd. But not if you change the distribution assumption.

Chebyshev's inequality says that if a random variable X has mean and variance ^2, then

Prob( |X - | >= k) 1/k^2.

Not only that, it is possible to construct a random variable so that the inequality above is tight, i.e. it is possible to construct a random variable X such that the probability of it being 50 standard deviations away from its mean equals 1/2500. However, this requires constructing a custom random variable just to make equality hold. No distribution that you run into in the wild will have such a high probability of being that far out from its mean.

I wondered what the probability of a 50-sigma event would be like with a random variable with such a fat tail that it barely has a finite variance. I chose to look at Student t distributions because the variance of a Student t distribution with degrees of freedom is /( - 2), so the variance blows up as decreases toward 2. The smaller v us, the fatter the tails.

The probability of a t random variable with 3 degrees of freedom being 50 sigmas from its mean is about 3.4 * 10^-6. The corresponding probability for 30 degrees of freedom is 6.7 * 10^-31. So the former is rare but plausible, but the latter is so small as to be hard to believe.

This suggests that 50-sigma events are more likely with low degrees of freedom. And that's sorta true, but not entirely. For 2.001 degrees of freedom, the probability of a 50-sigma event is 2 * 10^-7, i.e. the probability is smaller for = 2.001 than for = 3.

Here's a plot of the probability of 50-sigma events for a t distribution with degrees of freedom.

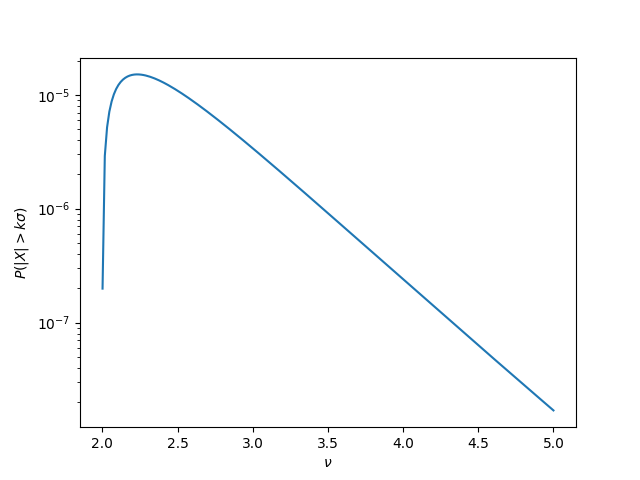
Apparently the probability peaks somewhere around = 2.25 then decreases exponentially as increases.

This isn't what I expected, but it makes sense after the fact. As increases, the tails get thinner, but also gets smaller. We have two competing effects. For less than 2.25 the size of matters more. For larger values of , the thinness of tails matters more.

The post 50 sigma events for t distributions first appeared on John D. Cook.