Yule statistics Y and Q
I recently wrote about the Yule-Simon distribution. The same Yule, George Udny Yule, is also known for the statistics Yule's Y and Yule's Q. The former is also known as the coefficient of colligation, and the latter is also known as the Yule coefficient of association.
Both measure how things are related. Given a 2 * 2 contingency table
with non-negative entries, Yule's Y is defined by
and Yule's Q is defined by
Both essentially measure how much bigger ad is than bc but are weighted differently.
The algebraic properties of these two statistics may be more interesting than their statistical properties. For starters, both Y and Q produce values in the interval (-1, 1), and each is an inverse of the other:
There's some simple but interesting algebra going on here. Define
This simple function comes up surprisingly often. It's a Mobius transformation, and it comes up in diverse applications such as designing antennas and mental math shortcuts. More on that here.
If we define
and
then W generalizes both Q and Y: setting p = 1 gives us Q and setting p = 1/2 gives us Y.
Given the value of W with subscript p, we could easily solve for the value of W with another subscript q, analogous to solving Q for Y and Y for Q above.
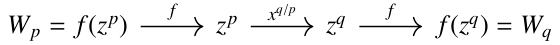
If you're expecting f-1 rather than f over the first arrow, you're right, but f is its own inverse so we could just write f instead.
Related postsThe post Yule statistics Y and Q first appeared on John D. Cook.