Catenary kiln

Will Buckner sent me an email with the following question recently. (I'm sharing this with permission.)

I am building a kiln using a catenary arch. The rear wall and front wall/door will be vertical and fill in the space under the arch, which has the dimensions of 41''W x 39.5''H. I need the area within this arch in order to calculate how many bricks I need to construct the two walls. Can you help me calculate that area?

Here's my solution. I fit a parabola and a catenary in part to check my work and in part to see how different they are.

Parabola

We'll start with a parabola as our warmup because it's easier.

Let w = 41 and h = 39.5. We want a quadratic function y(x) such that y(0) = h and y(w/2) = 0.

Assume y has the form

y(x) = b - ax^2

y(0) = h leads to the conclusion that b = h, and y(w/2) = 0. leads to

a(w/2) = h

And this leads to the final form.

y = h(1 - (2x/w)^2)

Catenary

Our catenary will have the form

y(x) = b - a cosh(x/a)

and again y(0) = h and y(w/2) = 0. These two requirements lead to the equations

b - a = h

and

b - a cosh(w/2a) = 0.

Then

b = h + a

and

h + a (1 - cosh(w/2a) = 0.

The latter equation cannot be solved in closed form, but it's easy enough to solve numerically. When I asked Mathematica to compute the root with

 FindRoot[39.5 + a - a Cosh[20.5/a] == 0, a]

it failed. Then I plotted the function, saw that the root was around 8.5, then gave Mathematica a hint.

 FindRoot[39.5 + a - a Cosh[20.5/a] == 0, {a, 8.5}]

Then Mathematica came back with

a = 8.475359432102444.

So the equation of our catenary is

y = h + a(1 - cosh(0.5 x/a))

where h and a are given above.

Plots

Here's a plot of both curves. The blue curve inside is the parabola, and the gold curve on the outside is the catenary.

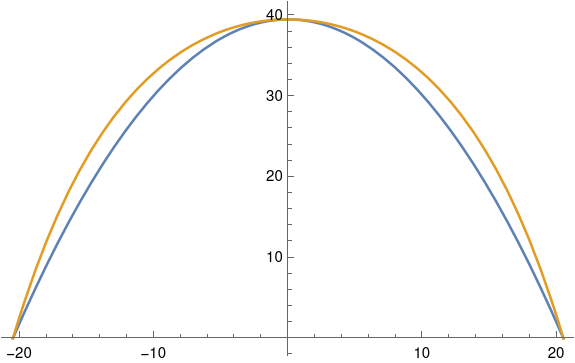
Here's the code that made the plot.

 Plot[{h (1 - (2 x/w)^2), h + a - a Cosh[x/a] }, {x, -w/2, w/2}]

Area

And now for the area, the thing I was asked to find. For the parabola

 Integrate[h (1 - (2 x/w)^2), {x, -w/2, w/2}]

returns 1079.67. For the catenary,

 Integrate[h + a (1 - Cosh[x/a]), {x, -w/2, w/2}]

returns 1166.56.

The number of bricks this will take is roughly the area of the arch divided by the area of a brick, but being more precise is a complicated question that depends on how much mortar you use, and how you use plan to use rectangular bricks to make a curved arch.

More catenary posts

• Best approximation of a catenary by a parabola
• Surface of revolution with minimum area
• A curious property of catenaries

The post Catenary kiln first appeared on John D. Cook.