Order statistics for normal distributions

The last couple posts have touched on order statistics for normal random variables. I wrote the posts quickly and didn't go into much detail, and more detail would be useful.

Given two integers n >= r >= 1, define E(r, n) to be the rth order statistic of n samples from standard normal random variables. That is, if we were to take n samples and then sort them in increasing order, the expected value of the rth sample is E(r, n).

We can compute E(r, n) exactly by

where and are the PDF and CDF of a standard normal random variable respectively. We can numerically evaluate E(r, n) by numerically evaluating its defining integral.

The previous posts have used

d_n = E(n, n) - E(1, n) = 2 E(n, n).

The second equality above follows by symmetry.

We can compute d_n in Mathematica as follows.

 Phi[x_] := (1 + Erf[x/Sqrt[2]])/2 phi[x_] := Exp[-x^2/2]/Sqrt[2 Pi] d[n_] := 2 n NIntegrate[ x Phi[x]^(n - 1) phi[x], {x, -Infinity, Infinity}]

And we can reproduce the table here by

 Table[1/d[n], {n, 2, 10}]

Finally, we can see how d_n behaves for large n by calling

 ListPlot[Table[d[n], {n, 1, 1000}]]

to produce the following graph.

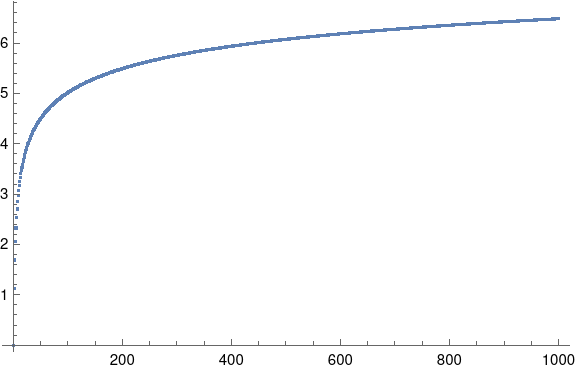
See the next post for approximations to d_n.

The post Order statistics for normal distributions first appeared on John D. Cook.