Transformations of Olympic rings
The previous post gave the details of how Mobius transformations
m(z) = (az + b)/(cz + d)
transform circles. The image of a circle under a Mobius transformation is either a line or a circle, and in our examples the image will always be a circle.
We start with an approximation of the Olympic rings
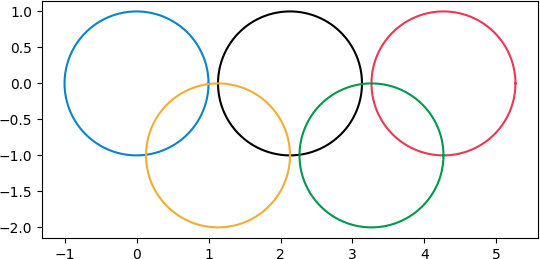
and then apply various transformations.
First we apply (z + 9)/(z + 10):
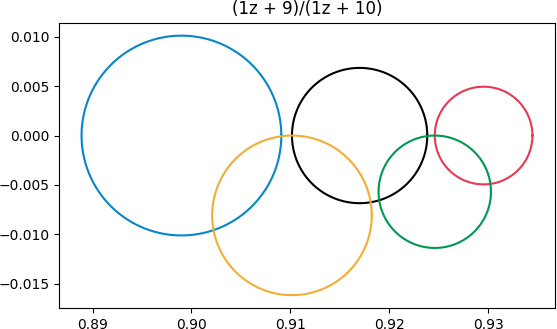
This transformation doesn't distort the rings too much because the rings are far from the singularity at z = -10. The blue ring is distorted the most because it's closest to the singularity.
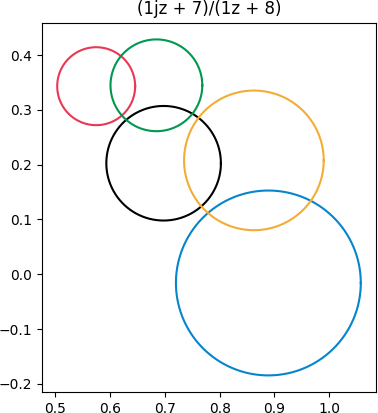
Next we apply (iz + 7)/(z + 8). Now we've moved the singularity a little bit closer, and we caused some rotation by using i as the coefficient of z in the numerator.
Finally, let's pick a transformation with its singularity inside the green circle, (z + 4)/(z -3 + i).
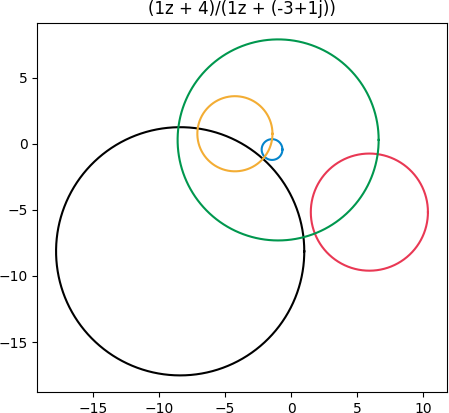
Now we see a lot of distortion. The blue and gold rings that were outside the green ring are brought inside. The complex plane is turned inside-out because of the singularity.
As before, the black and red rings still intersect the green ring. But what you can't tell from the graph is that the portion of these rings that was inside has been turned outside and vice versa.
Related postsThe post Transformations of Olympic rings first appeared on John D. Cook.