Helmholtz resonator revisited

We finished a bottle of wine this evening, and I blew across the top as I often do. (Don't worry: I only do this at home. If we're ever in a restaurant together, I won't embarrass you by blowing across the neck of an empty bottle.)

The pitch sounded lower than I expected, so I revisited some calculations I did last year.

As I wrote about here, a wine bottle is approximately a Helmhotz resonator. The geometric approximation is not very good, but the pitch prediction usually is. An ideal Helmholtz resonator is a cylinder attached to a sphere, and a typical wine bottle is more like a cylinder attached to a larger cylinder. But the formula predicting pitch is robust to departures from ideal assumptions.

As noted before, the formula for the fundamental frequency of a Helmholtz resonator is

where the variables are as follows:

• f, frequency in Hz
• v, velocity of sound
• A, area of the opening
• L, length of the neck
• V, volume

The opening diameter was 2 cm, the neck length 9 cm, and the volume 750 cm^3. All these are typical. The predicted frequency is f = 118 Hz. The measured frequency was 106 Hz, measured by the Sonic Tools phone app.

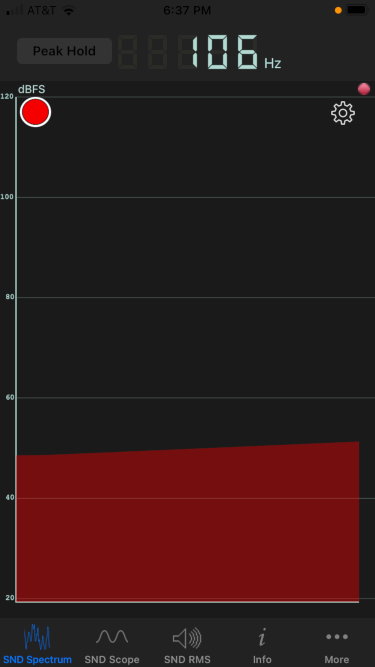
The actual frequency was about 10% lower than predicted. This is about a whole step lower in musical terms. I could certainly hear an interval that large if I heard the two pitches sequentially. But I don't have perfect pitch, and so I'm skeptical whether I could actually notice a pitch difference of that size from memory.

The post Helmholtz resonator revisited first appeared on John D. Cook.