Eliminating a Bessel function branch cut
In an earlier post I looked in detail at a series for inverse cosine centered at 1. The function arccos(z) is multivalued in a neighborhood of 1, but the function
arccos(z) / (2 - 2z)
is analytic in a neighborhood of 1. We cancel out the bad behavior of inverse cosine at 1 by dividing by another function with matching bad behavior.
We can do something similar with Bessel functions. In general, the Bessel function J has a branch cut from - to 0. But the function
J / z
is entire, i.e. analytic everywhere in the complex plane. From a certain perspective-namely the perspective advocated by Bille Carlson (1924-2013)-we got the definition of Bessel functions (and other functions) wrong. Carlson's book Special Functions of Applied Mathematics shows how many special functions can be defined in terms of a smaller number of functions with fewer branch cuts. This simplification revealed symmetries that hadn't been noticed before.
Here's a plot of J1/3(z). Height represents magnitude and color represents phase.
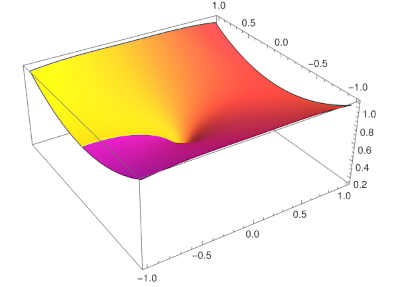
This was produced using the Mathematica command
ComplexPlot3D[BesselJ[1/3, z], {z, -1 - I, 1 + I}]The abrupt change from purple to yellow along the negative real axis shows the discontinuity in the phase at the branch cut. You can also see a hint of the cusp at the origin.
Here's a plot of J1/3(z) / z1/3.
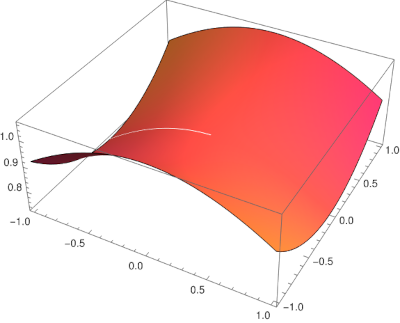
This was made using
ComplexPlot3D[BesselJ[1/3, z]/z^(1/3), {z, -1 - I, 1 + I}]The white streak is an artifact of the branch cuts for J1/3(z) and for z1/3. The branch cut in their ratio is unnecessary.
Related postsThe post Eliminating a Bessel function branch cut first appeared on John D. Cook.