Simultaneous root-finding

In 1891 Karl Weierstrass developed a method for numerically finding all the roots of a polynomial at the same time. True to Stigler's law of eponymy this method is known as the Durand-Kerner method, named after E. Durand who rediscovered the method in 1960 and I. Kerner who discovered it yet again in 1966.

The idea of the Weierstrass-Durand-Kerner method is to imagine you already had all but one of the roots and write down the expression you'd use to find the remaining root. Take a guess at all the roots, then solve for each root as if the remaining roots were correct. Iterate this process, and hopefully the process will converge on the roots. I say hopefully" because the method does not always converge, though it often works very well in practice [1].

Here's a Python implementation of the method for the special case of 4th degree polynomials. The general case is analogous.

 def maxabs(a, b, c, d): return max(abs(a), abs(b), abs(c), abs(d)) # Find roots of a 4th degree polynomial f # starting with initial guess powers of g. def findroots(f, g): p, q, r, s = 1, g, g**2, g**3 dp = dq = dr = ds = 1 tol = 1e-10 while maxabs(dp, dq, dr, ds) > tol: dp = f(p)/((p-q)*(p-r)*(p-s)); p -= dp dq = f(q)/((q-p)*(q-r)*(q-s)); q -= dq dr = f(r)/((r-p)*(r-q)*(r-s)); r -= dr ds = f(s)/((s-p)*(s-q)*(s-r)); s -= ds return p, q, r, s

Lets apply this to the polynomial

(x^2 + 1)(x + 2)(x - 3)

whose roots are i, -i, -2, and 3.

 f = lambda x: (x**2 + 1)*(x + 2)*(x-3) findroots(f, 1 + 1.2j)

Here is a plot of the iterates as they converge to the roots.

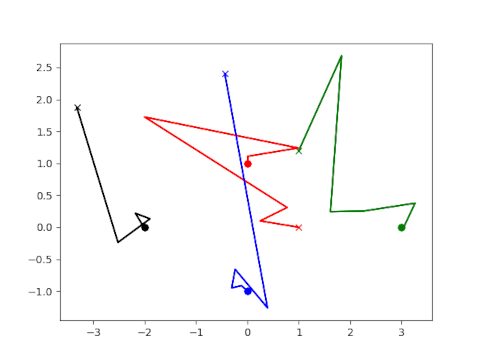
Each color corresponds to a different root. Each starts at the initial guess marked with * and ends at the root marked with a circle.

[1] Bernhard Reinke, Dierk Schleicher and Michael Stoll. The Weierstrass-Durand-Kerner root finder is not generally convergent. Mathematics of Computation. Volume 92, Number 339. Available online.

The post Simultaneous root-finding first appeared on John D. Cook.