Conformal map of ellipse interior to a disk
This post will present the conformal map between the interior of an ellipse and the unit disk.
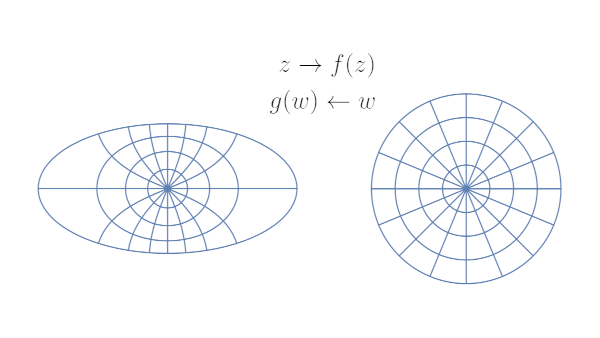
Given an ellipse centered at the origin with semi-major axis a and semi-minor axis b. Will will assume without loss of generality that a^2 - b^2 = 1 and so the foci are at 1.
Hermann Schwarz published the conformal map from the ellipse to the unit disk in 1869 [1, 2].
The map is given by
where sn is the Jacobi elliptic function with parameter k^2. The constants k and K are given by
where 2 and 3 are theta constants, the value so the theta functions 2(z, q) and 3(z, q) at z = 1.
Conformal maps to the unit disk are unique up to rotation. The map above is the unique conformal map preserving orientation:
The inverse of this map is given by
The inverse of the sn function with parameter m can be written in terms of elliptic integrals.
where F is the incomplete elliptic integral of the first kind and m is the parameter of sn and the parameter of F.
PlotI wanted to illustrate the conformal map using an ellipse with aspect ratio 1/2. To satisfy a^2 - b^2 = 1, I set a = 2/3 and b = 1/3. The plot at the top of the post was made using Mathematica.
Related posts- NASA and conformal maps
- Comparing Jacobi functions and trig functions
- Conformal mapping and Laplace's equation
- Numerically evaluate a theta function
[1] H. A. Schwarz, Uber eigige Abbildungsaufgaben, Journal fur di reine und angew. Matheamatik, vol 70 (1869), pp 105-120
[2] Gabor Szego. Conformal Mapping of the Interior of an Ellipse onto a Circle. The American Mathematical Monthly, 1950, Vol. 57, No. 7, pp. 474-478
The post Conformal map of ellipse interior to a disk first appeared on John D. Cook.