Approximating pi with Bernoulli numbers
In a paper on arXiv Simon Plouffe gives the formula
which he derives from an equation in Abramowitz and Stegun (A&S).
It took a little while for me to understand what Plouffe intended. I don't mean my remarks here to be criticism of the author but rather helpful hints for anyone else who might have difficulty reading the paper.
He says Here the Bn are positive and n is even." This doesn't mean that the Bn are positive; it means that we should make them positive if necessary by taking the absolute value.
Plouffe says that he derives his estimate from an equation on page 809 of A&S, but at least in my copy of A&S, there are no equations on page 809. I believe he had in mind equation 23.2.16, which is on page 807 in my edition.
This equation says
The first inequality in the paper does not appear directly in A&S but can be derived from the equation above. The approximation for at the top of the post approximates (2n) by 1. You could obtain a better approximation for by using a better approximation for (2n), which Plouffe does, retaining the first few terms in Euler's product representation for the zeta function.
How good is the approximation above? Plotting the approximation error on a log scale gives nearly a straight line, i.e. the error decreases exponentially.
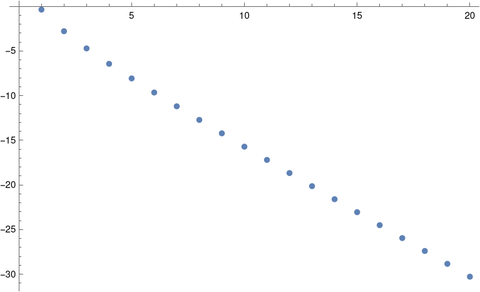
This plot was produced with the following Mathematica code.
f[m_] := (2 Factorial[2m] / Abs[BernoulliB[2m] 2^(2m)])^(1/(2m)) ListPlot[Table[Log[Abs[f[m] - Pi]], {m, 1, 20}]]Related posts- Euler product for sine
- Five posts on computing pi
- Special numbers (Bell, Bernoulli, Stirling, etc.)
- Why Euler's product can't be used to find zeros of zeta