Hyperbolic secant distribution
I hadn't run into the hyperbolic secant distribution until I saw a paper by Peng Ding [1] recently. If C is a standard Cauchy random variable, then (2/) log |C| has a hyperbolic secant distribution. Three applications of this distribution are given in [1].
Ding's paper contains a plot comparing the density functions for the hyperbolic secant distribution, the standard normal distribution, and the logistic distribution with scale 3/. The scale for the logistic was chosen so that all three distributions would have variance 1.
There's something interesting about comparing logistic distribution and the hyperbolic secant distribution densities: the former is the square of the latter, aside from some scaling, and yet the two functions are similar. You don't often approximate a function by its square.
Here's a plot of the two densities.
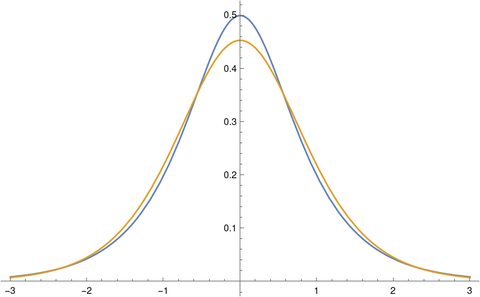
The hyperbolic secant density, the blue curve, crosses the logistic density around 0.56 and around 2.33.
The hyperbolic secant distribution has density
and the logistic distribution, as scaled in above, has density
and so
[1] Peng Ding. Three Occurrences of the Hyperbolic-Secant Distribution. The American Statistician , Feb 2014, Vol. 68, No. 1 (2014), pp. 32-35
The post Hyperbolic secant distribution first appeared on John D. Cook.